Light Travel Distance in an Exploding Universe

by John P. Pratt
27 Aug 2019, 1 Light (SR)

©2019 by John P. Pratt. All rights Reserved.

Index, Home

Contents

1. Background Research 2. Big Bang Universe 3. Big Grenade Universe 3.1 Low Velocity 3.2 High Velocity 4. Conclusion Notes

Light travel distances to high redshift celestial objects based on Hubble's Law have been misleading. A new method of estimating those distances is proposed.

Recently my nephew Robert Pratt asked me a straightforward question about the Big Bang theory. He probably asked me because of my having taught astronomy at the college level.[1] Essentially his question was, "How long did it take for the most distant galaxy to get where it was when the light left it which we now see?"

Edwin Hubble at 100-inch telescope.

"Nearly 14 billion years," I quipped. When I said that, I was combining two generally believed results from modern astronomy: (1) current Big Bang theory teaches that the Universe is about 13.8 billion years old,[2] and (2) the most distant galaxy appears to be moving away from us at nearly the speed of light, so according to the Big Bang model, it would have gone about 14 billion light years away from us.

He then repeated the question, spelling out the problem for me: "But if that galaxy took nearly 14 billion years to get where it was when the light left it, and it took almost another 14 billion years for that light to get to us, wouldn't that make the universe nearly 28 billion years old?"

He was right! It immediately sunk in that my answer could not possibly be consistent with Big Bang theory because then the universe would be much older than 14 billion years (byr). Even though I have taken special and general relativity classes and done most of the simple textbook problems, a cold chill ran through me as I realized I did not have a ready answer to Robert's question. It was time to both think this out myself as well as research what current answers to this question are.

This article is an attempt to answer what is herein called "Robert's Question": "At what time and distance was the light emitted which we see from distant objects?" The article does not address the validity of Big Bang theory, but only seeks an answer to Robert's Question within the Big Bang framework. It begins with some background research on the subject, then reviews Big Bang theory, and then proposes a simpler model of an exploding universe to derive an approximate answer to Robert's Question.

Table 1. Why even list these distances?

My first step was to check on what the current most distant galaxy known is. According to the current list of the most distant objects Wikipedia (the first ten entries being reproduced in Table 1), it is GN-z11 a galaxy with a "Light travel distance" of 13.39 billion light years (bly).[3]

But that "light travel distance" is a disaster because it leads to the very answer I gave Robert, which could not be true if the universe is indeed 13.8 byr old! Here the question need not be about anything going faster than light, it is merely a question about giving a self-consistent story about the age of universe.

Then the huge disclaimer was noticed in the Wikipedia table! A footnote to the column of "Light travel distances" states: "The tabulated distance is the light travel distance, which has no direct physical significance." What?? What does that mean? Of course a light travel distance should have physical significance!! It should be the distance where the galaxy was away from us when the light left that distant galaxy! That column should contain the answer to Robert's Question! At first, it looked like it was the answer until that footnote was noticed which made the entries meaningless! It looks like someone had thought of inconsistencies raised by Robert's Question, but listed those distances anyway for lack of anything better. On second thought, it looks more like one person listed the distances believing they were meaningful and another person added the footnote! This was getting curiouser and cursiouser![4]

That disclaiming footnote gave a bread crumb trail of references to follow, which led to what appears to be the authoritative article on the subject in 2013 by Prof. Edward L. (Ned) Wright of UCLA. He is definitively an authority, having been a science editor of The Astrophysical Journal, the premier profession journal in the field. His article is a plea to all astronomers to stop publishing light travel distances in newspaper releases, as it only leads to confusion! It began by noting that after lectures that some form of "Robert's Question" would often be asked. I was delighted to discover this article for surely it would explain the correct answer from an expert source. Then, to my dismay, this was the reason given for avoiding reference to light travel distances:

Distance is defined as the spatial separation at a common time. It makes no sense to talk about the difference in spatial positions of a distant galaxy seen 9.1 billion years ago and the Milky Way now when galaxies are moving.[5]

Georges Lemaitre.

What?? Surely he did not mean what he said! His explanation must, however, stand up to scrutiny as is. This definition of distance is unknown to me in physics. It is well known in relativity that two different reference frames moving relative to each other will measure times and distances differently. The usual definition of distance is defined as the spatial separation at a time in one reference system. Distance is not measured at a common time between two moving systems. Our system will measure a certain distance and time when the light left that galaxy and that galaxy will measure another position and time when that light left. Thus, Wright correctly states that there is no common time and hence it makes no sense to ask about a common distance. But that is not Robert's Question! It does not concern the time or distance in the other galaxy. It makes perfect sense to ask the question about how far was that galaxy from us when its light left!

It was at this point that my preliminary research abruptly ended. I decided to try to calculate the distance myself, if for no other reason than to fail and find out why apparently no one else has done it. Today's sophisticated Big Bang theory is extremely complicated, with all kinds of tweaks and options added to avoid problems of inconsistency. They include Einstein's theory of gravity with various proposed updates, dark matter, and dark energy, all to help the equations to come out with a more believable story. One method that can be useful in solving a hard problem is to simplify the problem to be one that is well understood and solvable. Hopefully the simplification will retain the essence of the actual problem so that its answer will be an approximation of the actual answer. Some great physicist, perhaps Phil Morrison, said something like, "Physics is the study of what can be ignored."[6] In order to come up with a simpler model, let's first review basic Big Bang theory and then use a simplified model to approximately answer Robert's Question. The actual purpose of this article is mostly to introduce the simplified model in case it helps the understanding of others as it did mine. Later, others can argue with my result on the grounds that major influences and forces (like gravity!) have been ignored in my simple model. All that is hoped is for this article to offer a starting point, perhaps only slightly better than listing distances which have no physical significance!

Much of the following summary is condensed from the excellent "Big Bang" Wikipedia article.[7] Albert Einstein introduced his general theory of relativity in 1915, which was mostly about explaining gravity geometrically. The theory predicts an expanding universe and some other physicists explored the implication that space itself was expanding. The most notable was perhaps Georges Lemaitre who in 1927 proposed that the expansion could perhaps be traced backward in time to an original "cosmic egg". That was a great name because eggs do not explode but are hatched in an orderly fashion, but unfortunately that name was rejected for the flashier name "Big Bang", which has led to much misunderstanding.

Fig. 1. Raisin bread like expanding space.

Most did not take his theory seriously until in 1929 Edwin Hubble discovered that many galaxies were indeed moving away from us with a velocity proportional to their distance, exactly as predicted. That is, a galaxy which is twice as far away is moving away from us about twice as fast. Hubble had only shortly before been able to determine their distances as being outside of our galaxy. He could measure the speeds by the shifts of the spectral lines toward the red ("redshifts") which indicated their velocities away from us. Those velocities were indeed proportional to their distances, which became known as Hubble's Law. That was a compelling fulfillment of a theoretical prediction and the "Big Bang" theory was born. That name is unfortunate because it suggests an explosion of matter through space, whereas the theory is really about the expansion of space itself,[8] carrying matter with it. The idea is often illustrated by raisins in the dough of a rising loaf of raisin bread. As shown in Figure 1, they get farther apart with a velocity proportional to the distance between them, but it is the matrix they are in which is expanding. Note that the raisins were not shot out in an explosion, but bread is being created in an orderly fashion.

Here we need not attempt to capsulize all of the additions, bells, and whistles which have been added to the theory to make everything tell one consistent story which makes it look like we understand it. That can be avoided because this article is about replacing that theory with a much simpler one which has most of the characteristics of the full-blown theory.

Halton "Chip" Arp.

One weakness in Big Bang theory should here be noted because most discussion of this problem has apparently ended in favor of the current theory. A redshift is only known to mean that the emitting source is receding from the observer. In the case of a celestial object, it does not mean that the velocity is necessarily due to the expansion of space. Stars and galaxies have their own motion moving around in space in addition to the theoretical space expansion. In the 1970s, when I was getting my PhD in astronomy, there was much discussion of quasars, the star-like objects which had super high red-shifts, which are now mostly believed to be distant galaxies (or their centers). If their redshifts are "cosmological" (meaning "due to the expansion of the universe") then they presumably would follow Hubble's law, which means that they are exceeding far from us. In turn, that would mean they would have to be incredibly bright in order for us to see them at all.

A long-time astronomer at Hale Observatories named Halton Arp produced an entire atlas of photographs showing that several pairs of galaxies which were clearly interacting with each other had very different redshifts, which would break Hubble's Law because they were at the same distance. Moreover, many quasars appear to be right next to nearby much closer galaxies, suggesting that they might have been shot out of those galaxies at the very high speeds. That proposal was silenced with the question, "If so, why do all of them have redshifts, with not even one blueshift, which would be expected if half of those quasars were coming toward us?" No one with credentials had an answer to that question nor could explain how one galaxy could be "shot out" of another,[9] so Arp was denied telescope time in the U.S. because of being a trouble maker by not toeing the party line. He chose to continue work at the Max Planck Institute for Astrophysics near Munich, Germany, to do his observations![10] Now he is rarely mentioned in articles at all!

Let us now turn to a simplified theory to get an approximate answer to Robert's Question.

3.1 Low Velocity

A hand grenade explodes into many pieces.

Imagine an ant named Hubble who was on a hand grenade which exploded. To keep it simple, this was done in a place with no gravity in empty flat space (no dark energy or matter), which means that each of the fragments went out in a straight line from the place of explosion, with each at a velocity which remained unchanged forever for that fragment. This is the "exploding universe" referred to in the title of this article, not the Big Bang universe, which is not exploding, but expanding.

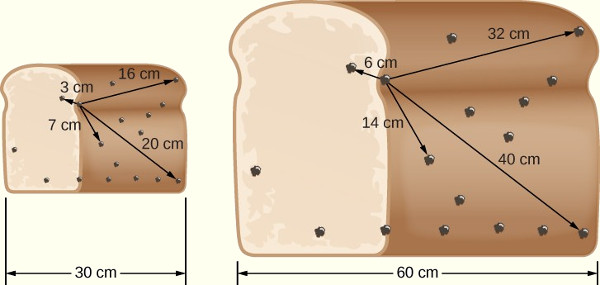
Hubble survived and decided to study the other fragments of the explosion. He was on the piece indicated in Figure 2. All of the pieces were flying apart from each other, and were going various speeds because they were different sizes and received different amounts of the explosive energy.

The first thing he noticed was that all of the other pieces seemed to be going directly away from him. He also felt like he was at rest because, just like someone in a jet plane can feel at rest, his piece was moving at a constant velocity. Thus, he felt like he was at the center of this exploding universe because he observed that all of the other pieces were moving directly away from him. Proving that is left as an exercise for the physics student (just draw a velocity vector diagram).

Fig. 2. An exploding universe.

The next thing the ant noticed is that at any instant, the farther a fragment was away from him, the faster it was going. In fact, it was a direct proportion, meaning that if one piece was twice as far away as another, then its "recessional velocity" away was twice as fast. He called it Hubble's Law. Notice that this is exactly analogous to the raisin loaf expanding space universe illustrated in Figure 1. In both, the velocities of all the raisins/fragments are directly away from any one raisin/fragment, and the velocities of separation between the two illustrations are proportional to the distances.

After some time Hubble realized that his law should have been obvious because

Distance = Velocity x Time. (Equation 1)

That is, the distance that something moves equals its speed multiplied by the time it is moving. For example, a car going at a speed of 75 miles/hour will go 150 miles in 2 hours: 75 miles/hour x 2 hours = 150 miles. Because all of the pieces started at the same time, then time is same for all and so the fragments with twice the speed will go twice as far in that same time since the explosion.

Hubble the ant had already his own equation for this, somewhat backwards from that usual equation relating velocity and distance. He decided to leave it in his more confusing original form. He wrote it like this:

Velocity = H x distance. (Equation 2)

He called the constant H the Hubble constant of proportionality between the distance to a fragment and its speed away from him. Only after a while did he realize that 1/H was actually just the time since the explosion. (To see this, just compare the two above equations, remembering that the time of flight for each fragment is the same.) That is why H was a constant: it was the age of this universe of fragments! It is important to understand that it did not matter which fragment he looked at, H was the same for all pieces because 1/H was the time since the explosion. He did not have to look at the farthest pieces to determine the age of his universe.

Another point that he realized is that this so-called "constant" H is only a constant for the moment that he happened to look at all of the fragments. It was a constant all through space for one instant. It took a while for it to sink in that 1/H was nothing more than the time since the explosion! Then he understood that if he had waited twice as long after the explosion to measure the velocity of the fragments, then the time of flight would have been twice as long, and the distances would all have been twice as far, so H would only have been half as big (to multiply times the distance to get the same velocity). It was really the fragment velocities, not H, which were each constant in time!

Finally, he realized that he could determine whether or not he was really in the center of this universe. He realized that if he were not at the center, then there would be more fragments on one side than the other. When he counted fragments in different directions, he correctly concluded that he was on a piece flying away from the true center (as in Figure 2), and that whatever piece he might have been on would have appeared to be the center (because all other fragments would appear to be going away from it).[11]

This very simple example of an explosion fits well with what a real astronomer named Edwin Hubble was seeing in 1929! As described above, the universe looked like it could have come from a huge explosion or expanding space. The main purpose of this simple analogy to a hand grenade is to show how much an actual explosion does in fact model the expanding space, like the raisin bread analogy, of the real Big Bang theory. Thus, simple calculations can hopefully give approximately correct answers. One indication that this method might not be too far off is the currently measured real Hubble constant 1/H₀ = 14.4 billion years (byr), whereas the currently believed aged of the universe is believed to be 13.82 byr.[12] Thus, they are close enough to being the same that both can be rounded off to 14 byr!

Now let us consider a high velocity super grenade!

3.2 High Velocity

Let us now look at the same exploding hand grenade problem again and just add one more factor. Let us see what happens if the velocities of some of the exploded fragments are near the speed of light. That is required to answer Robert's Question. Now we will need to use relativistic equations. But let us still ignore the effects of gravity, which are negligible for the attraction of the fragments of a hand grenade to each other.

The equations of special relativity apply to systems moving at constant velocities relative to each other, not accelerating or decelerating. Equations called the Lorentz transformation show how time and space look in one system moving at a constant velocity to another system. In other words, they are useful if a rocket is flying by you at constant velocity, and both you and its passengers observe the same phenomenon, then these equations show how it would appear in both systems.

But we do not need the time and space equations of relativity to answer the question being considered in this article. Robert's Question is "At what time and distance was the light emitted which we see from distant objects?" All of the observations are done in our frame of reference on earth, so the Lorentz transformation is not needed for the time and distance! Even at high velocities, the answer is as simple as Robert first suggested using Newtonian physics: the time from the beginning of the universe to when the light from a galaxy is emitted plus the time it takes to get from that galaxy to us should add up to 13.82 byr. If it does not (as with the distances/times listed in Table 1), then there is a problem, which is the purpose of this article to solve. There is, however, one place where we do need one relativistic equation, as discussed next.

Fig. 3. Redshifted hyrdogen spectral dark absorbtion lines.

Consider the light from the most distant galaxy we can see. Let us consider that the galaxy is instead a fragment of our Big Grenade. The distances to galaxies are calculated by Hubble's Law, assuming it holds everywhere and that everything in the universe came from the same beginning point. That is true for the exploding grenade. Hubble's Law converts speeds away from us into distances from us. Velocity of recession is in turn determined by the redshift of light of known wavelength to what is actually observed. For example, it is known that a hydrogen atom has a series of sharp spectral lines at very precise wavelengths, as shown in the bottom spectrum of Figure 3. If those lines are seen in a star, the entire group of lines can be shifted over into redder colors, as in the second spectrum up in Figure 3. This "redshift" tells us that the star is moving away from us. If the star were moving toward us, all of the lines would be slightly shifted towards the blue. The ratio of the change in wavelength (λ' - λ₀ in Figure 3) wavelength to the laboratory wavelength λ₀ is called the redshift, denoted by the letter "z". The upper rows of spectra show that galaxies are going away from us at much larger velocities than stars because they have larger redshifts. Compare the top redshift shown in Figure 3, which is about z = (590 nm - 430 nm)/430 nm = 0.37, to the redshifts in Table 1. The lowest listed there is 7.5, about 20 times that of the "very distant galaxy" in Figure 3, which shows just amazing those Top Ten redshifts are. They are literally "of the charts"! They were extremely hard to measure at all!

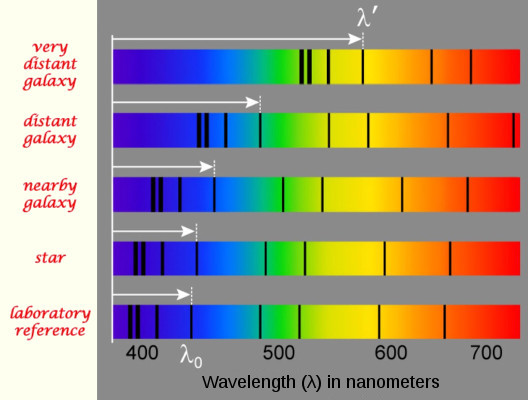It is for the interpretation of redshifts as recessional velocities that a relativistic equation is needed. That is because in this case, two different reference frames are compared. First, it is assumed that the rest wavelength λ₀ is the same in either our system or the galaxy, where the inhabitants feel they are at rest. The wavelength of a spectral line in our lab (at rest) is compared to the wavelength (λ') of that line in the galaxy moving away from us at a huge velocity. Indeed, it is because two reference frames are involved the red shift occurs at all. Thus, the special relativity equation for converting redshift to velocity must be used even in this simplified model.

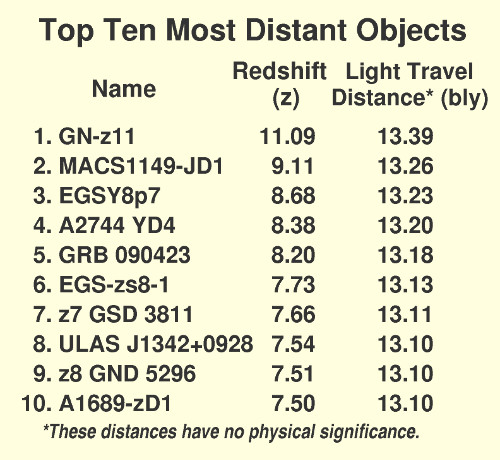
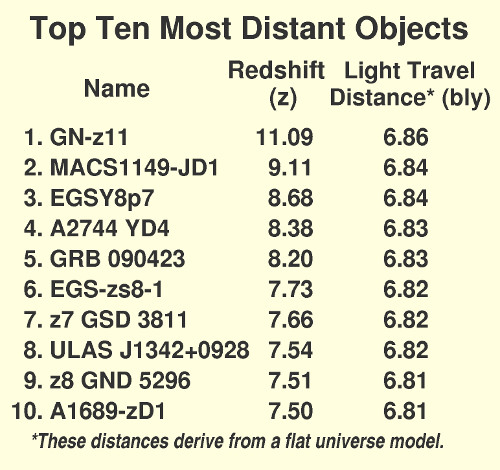
The Big Bang theory assumes all redshifts of very distant galaxies result from the motions due to the expansion of space. That is a big assumption, which Hubble himself was careful not to make, because he knew there are other causes of redshifts. Let us use that Big Bang assumption to answer Robert's Question. The redshift z of the farthest galaxy known currently is 11.09 (see Table 1), which is about 10 figure widths off to the right in Figure 3! That redshift can then be converted into a velocity using the equations of special relativity to get a recession velocity v of .98641 of the speed of light.[13]

Now let us assume one grenade fragment is going that speed, with a Hubble constant for the Big Grenade universe equal to what is agreed by most to be the current value for our universe, 1/H = 13.82 byr. That would mean that the total age of the Big Grenade universe is 13.82 byr, which must equal the time for the fragment to have arrived at the point at which the light was emitted which we saw plus the time for that light to get to us. Let us solve this problem in general for any z, and hence any v. As we solve it, note that we will not use Hubble's Law per se, but instead A, the current age of the universe when the light from the distance object is received. Thus, A = 13.82 byrs.

Let us now solve the problem: Find the distance d of a fragment with recessional velocity v in the Big Grenade Universe when it emitted the light seen later at time A, the age of the universe when the observation was made. Also find the time t when that light had been emitted.

Fig. 4. Light Travel Distance.

As shown in Figure 4, the distance d from the ant's location to where the light was emitted is the same as the distance back (because he can be considered to be at rest). According to Equation 1, the distance on the trip away is simply vt, the (constant) velocity times the time to arrive at the point seen. Similarly, that same distance d coming back equals c(A - t), again simply being the the velocity of light c times the time for the trip back. Note that this problem is not complicated by expanding space because it concerns two fragments of an exploding Big Grenade. Equating those two distances and then solving for t and d yields:

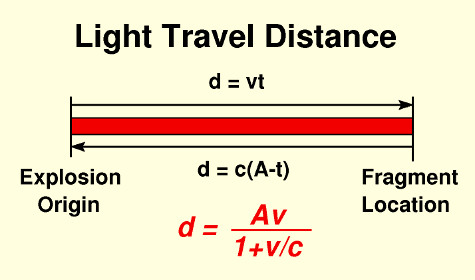t = A/(1+v/c), and
d = Av/(1+v/c).

In this simplified universe, those equations give the time and distance to the point where the distant fragment was seen. That is, they are the answer to Robert's Question. And these equations work for even high velocities. If the fragment were going the speed of light, then 1 + v/c would be 2, meaning that the fragment would have been seen at half of the age of the universe, which makes sense.

But is this answer indeed a good approximation to the correct answer in the Big Bang model? Others may decide that issue. One argument in favor of this answer is that even though it does not include the many features of the Big Bang Universe, the age of the Big Bang model of 13.8 byr is close to the current value of 1/H₀ = 14.4 byr, which means with all the nuances added to the Big Bang Universe, they did not change the age of the universe much from the simplified model of 1/H₀.

Table 2. Proposed reasonable distances.

When applying this new distance equation to the Top Ten most distant objects, and using A = 13.82 byr, the best estimate for the age of the universe, the results are shown in Table 2. A second feature in favor of these results is that now those seeing them will not ask Robert's Question because there is no problem and the footnote can say that they are based on an approximation rather than that the distances listed are meaningless!

There is perhaps one more concern which should be raised before adopting these new equations as good approximations. If the fastest receding galaxies at essentially the speed of light are seen by us as they looked 6.9 byr years ago, does that leave them enough time to have developed?

To answer that question, we need to turn to the Lorentz transformation equations because we are asking about the perceived time in that galaxy moving very fast relative to us. Here the simple Big Grenade Universe model will be used so see if it yields a reasonable approximation. Calculating the age of the first galaxy on the Top Ten list (which would be the youngest age at observation) the answer is that even though it would be 13.82 - 6.86 = 6.96 byr old according to our view, it would be a mere 1.14 byr in its own frame,[14] which it considers to be at rest, even as we consider ours at rest. That is exceedingly young for a galaxy. Is that a problem? Apparently not, because one galaxy known is believed to be only 0.5 byr old.[15] Thus, this new equation is offered as a reasonable approximation to the light travel distance until a better one becomes available.

Notes