Fibonacci Growth Model for Fellowships

by John P. Pratt
25 Feb 2020, 1 Temple (SR), Celestial (S)

©2020 by John P. Pratt. All rights Reserved.

Index, Home

Contents

1. The Fibonacci Sequence 1.1 Doubling Growth 1.2 Fibonacci Growth 2. Fellowship Growth 2.1 Geography 2.2 Clergy 2.3 Friendships 2.4 Fibonacci Growth 3. Conclusion Notes

The Fibonacci Sequence, so common in nature, provides a possible organization growth model.

Table 1. Fibonacci Sequence.

There is a series of numbers called the Fibonacci Sequence found in many living organisms in nature which seems to govern many processes. It is the natural consequence of certain growth patterns. The source of these numbers in nature is discussed, and examples are given and compared to other rates of growth. Finally a model is presented, based on that sequence for the growth of an organization such as multilevel marketing or religious fellowships, where an organization is designed to grow but is also constrained to meet in small groups, usually in homes. The method proposes when and how the growing group should be divided, such as a pride of lions.

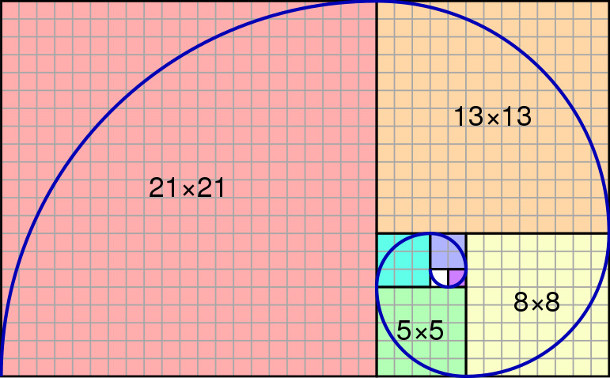
The Fibonacci Sequence is a series of numbers which is created with the number 1 and then adding to it the last number in the series. The second number is also 1 because there was no number preceding it, but then the next number is 2, arrived by summing 1 + 1. The next is 3, being 2+1, and the next is 5, derived from 3+2. Table 1 shows a list of "Fibonacci numbers", referring to members of the sequence. It can be seen that each number is the sum of the two immediately above it. For example, the last one shown is 144, which is the sum of the two above it: 55 + 89. The Fibonacci Sequence is one type of geometric series, even as doubling each number also is, because the ratios of succeeding numbers approach the fixed ratio of 1.618, called the "golden number". There are several excellent introductory articles about the Fibonacci Sequence.

So what is it that differentiates this series of integers such that it is found throughout nature in the growth of living organisms? To understand this, let us compare two kinds of growth, both of which are found in nature: doubling growth and Fibonacci growth.

1.1 Doubling Growth

Table 2. Doubling vs Fibonacci Growth.

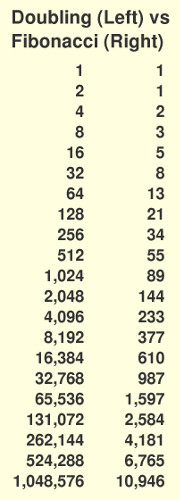Another example of doubling is the number of your ancestors, if they did not marry relatives. You have two biological parents, and each of them has two parents, so you have four grandparents. Similarly, you have eight great grandparents and sixteen great-great grandparents. Again, going back twenty generations could lead to over a million ancestors if none married even distant relatives in that group.

1.2 Fibonacci Growth

Now let us consider similar examples, but instead of Fibonacci growth. This is much more common in nature because larger plants and animals do not divide into half, but instead have immature offspring. Plants can create seeds or send out runners as do strawberries. This reproduction may or may not involve males and females. For the purposes of this article, where the results are to be used growing an organization, it is assumed that all members are the same type, such a people, salesmen, etc.

Growth which involves time for offspring to become mature leads to what is called herein "Fibonacci growth". Depending on the details of the number of offspring per cycle and the time for them to mature, it can lead to sequences other than the classic Fibonacci series. It is slower than doubling because of the time required for the young to mature.

Table 3. Fibonacci Growth.

Let us consider the example of Fiboncci growth which indeed leads to a Fibonacci sequences of members. Let us suppose there are three stages to the life of each member of the organization or population being considered: infant, youth, and adult. If the organization is a sales group, those stages might correspond to levels named distributor, team lead, and supervisor. In a religious fellowship, the levels might be called "newcomer" (novice or new convert as in 1 Tim. 3:2,6), "teacher", and "disciple", and in a trade they could refer to "apprentice", "journeyman", and "master". The names "infant", "youth" and "adult" are used in Table 3 to show how these levels lead to the Fibonacci series.

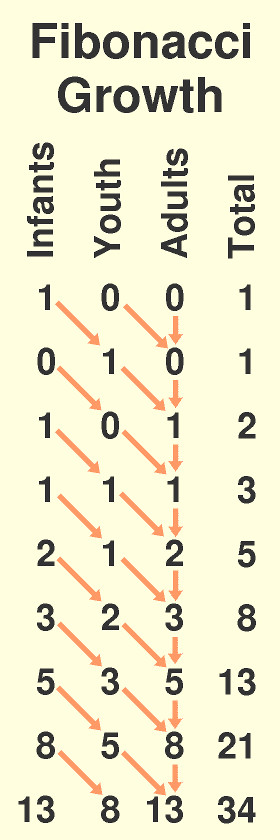Let us begin with one infant. After one growth cycles it becomes a youth. After another it becomes an adult and produces an infant. Thus, if all growth cycles are synchronized, there will be two members of the group at the beginning of the third cycle: one adult and one infant (see Table 3). At cycle 4 the adult produces a second infant, so now the total is 3: 1 adult, 1 youth and 1 infant. At cycle 5 there are now 2 adults, 1 youth, and 2 new infants because both adults produce an infant, for a total count of 5. At each cycle, all of the youth become adults (bearing new infants) and all of the infants move up to youth. At each cycle there will be added a new group of adults equal to the last number of youth, and a new number of infants equal to the new number of adults.

Table 3 shows how this pattern continues. The arrows pointing diagonally down indicate that all of the infants grow to become youth and then the arrow continues down to the next line to show that all of the youth become adults, which in turn adds to the number of adults. Looking at pattern of the table, we see that each column also forms a Fibonacci Sequence. And in particular it can be seen why each new total equals the sum of the last two numbers: the last number equals the total number from the previous cycle plus the number of new infants, which equals the number from two cycles before.

Fig. 1. X chromosome ancestors form a Fibonacci Sequence.

Let us consider one more example of this kind of growth in nature. Consider a case about your ancestors similar to that mentioned in the last section. Men have an X and a Y chromosome, whereas women have two X chromosomes. Thus, the man must inherit his Y from his father because his mother has none. On the other hand, a person can inherit the X chromosome from either his father or mother. The question arises, how many possible ancestors does a person have that could have contributed to their X chromosome?

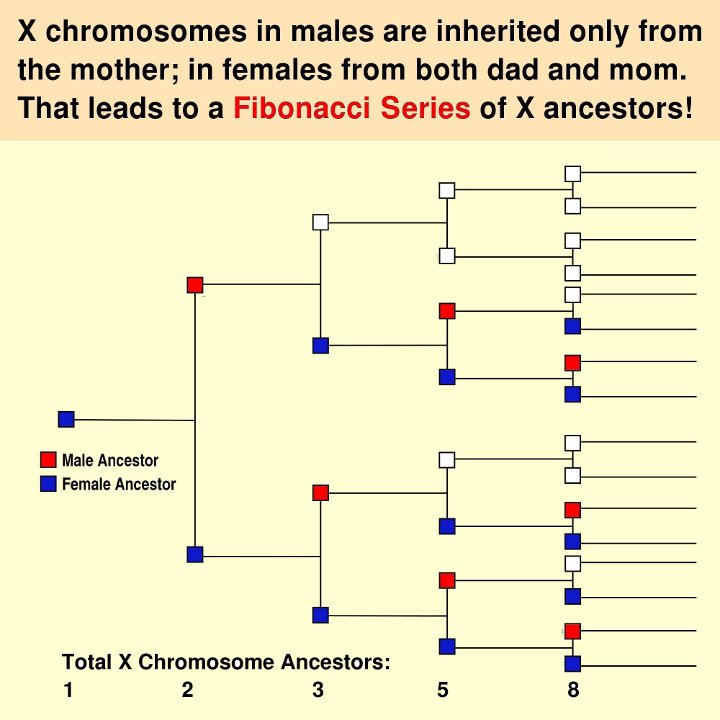The answer turns out to produce a Fibonacci Sequence of possible ancestor contributors to the X chromosome, as shown in Figure 1. Note that this result does not depend on any assumptions about all of the members living or producing only one offspring per cycle. The "bottom line" is that, as shown in the bottom line of Table 2, the number of X chromosome ancestors going back 20 generations is only about 11,000 rather than a million!

2.1 Geography

The phalanges of the fingers have Fibonacci lengths. A fist makes a Fibonacci spiral.

One important consideration is geography. Because a fellowship meets in the home of one of its members, when the group becomes too large it could use the geographic locations of the homes of its members are one criterion to be used for division into two parts. If this were the only criterion, however, friends could be torn apart, newcomers could be left without the instruction and guidance of more experienced teachers and disciples.

2.2 Clergy

It is important that each division has a priest or whatever level of ecclesiastic authority is required to perform ordinances such as baptism of new converts and fellowship rites such as the sacrament of the Lord's supper. If tithes are to be collected, a person with that authority (or the potential to receive it) must also be available.

2.3 Friendships

While it goes without saying that immediate families should not be broken up by the division of a fellowship, it may also be important that certain close friends be allowed to remain together. The idea of a fellowship is to have people worship together, help each other, and become of one heart and one mind. Very often a group of friends might be converted together, and perhaps they should stay together.

On the other hand, if the friendships are between the "disciples" (most solid in the faith) and also the top clergy, and those friends might be neighbors where they already have plenty of contact, it might be best to have those friends divided into separate fellowships in order better to serve the group. These can be tough decisions.

2.4 Fibonacci Growth

While these considerations already mentioned are not new to those who have wrestled with the problems of division from growth, it is here proposed that the Fibonacci Sequence might also be a valuable consideration.

8 and 13 opposing pine cone spirals.
(Click to enlarge.)

The first concept is to try to divide near Fibonacci numbers. For the purpose of this example of a fellowship, the three levels of members will be called newcomers, teachers, and disciples. When the total number of baptized members (meaning old enough to be accountable to God) reaches a Fibonacci number that is near the maximum number which can meeting in the same room of the home, then it is time to split the fellowship. Let us say that number is 21. Table 3 shows how any Fibonacci number in the right column approximately splits into expected numbers of newcomers (called Infants in the table), teachers (Youth) and disciples (adults). Try to put each member into one of those three groups and then see if the numbers in the fellowship approximately equal what can be expected. That is, are there about 8 newcomers, 5 teachers, and 8 disciples (see Table 3)?

Then try to divide the group of 21 into a group 13 and 8, the next two lower Fibonacci numbers, using the first the criteria of geography, clergy, and friendships. Then check to see if each of the two new subgroups have the expected numbers of newcomers, teachers and disciples, as shown in Table 3. That is, does the group of 13 have about 5 newcomers, 3 teachers, and 5 disciples? Does the group of 8 have about 3 newcomers, 2 teachers, and 3 disciples?

This concept is similar to the division of a pride of lions. They need a certain number, usually about 15, to provide for the group. It must include 2 or 3 adult males for protection, perhaps 5 females for hunting together large animals such as giraffes, as well as the young to be cared for by the adults and to learn from their example.

All of these criteria are only guidelines and your situation may differ. At the least it is hoped that these ideas might be helpful in what is nearly always a difficult process.