Celestial Witnesses of the Meridian of Time

by John P. Pratt

Reprinted from Meridian Magazine (July 10, 2002)
©2002 by John P. Pratt. All rights Reserved.

Index, Home

Contents
1. The Day-Year Pattern
2. Enoch Calendar
3. Realignment Cycles
4. Enoch Realignments
5. Enoch Witness
6. Conclusion
Notes
The year of the Savior's birth has been uncertain to Bible scholars, but now the Enoch calendar has been discovered to be a second witness with the Hebrew calendar that Christ was born in the year 1 BC. It also testifies of many events of the latter days, including the upcoming Feast of Trumpets.

There has long been a controversy about just what was the year of the Savior's birth. Scholars cannot agree to within much better than a decade (about 8 to 1 BC), with most favoring 6-5 BC. The Lord gave the prophet Enoch a big clue, that Christ would be born in the "meridian of time" (Moses 7:46), most likely referring to a precise midpoint of earthly time. The Book of Enoch records that an angel also revealed to Enoch a special calendar, the Enoch calendar. The Lord also revealed another calendar, used by Moses, which became the modern Hebrew calendar.

When one counts years the same way as days, as the Lord seems to do, both of these calendars have a year which is indicated to be the "meridian of time." In the case of the Enoch calendar, the meridian has just been discovered to be indicated by the phases of the moon, accurate to within a tenth of a day over eight thousand years. Both calendars testify that Christ was born in 1 BC. That agrees with the traditional LDS interpretation of (D&C 20:1), that Christ was born 1,830 years before the LDS Church was founded on Tue 6 Apr 1830.

This article is the first of a three part series. The witnesses of these two calendars of the meridian of time is the principal topic for this month. Next month the Lord's apparent use of the Enoch calendar in the restoration of the LDS Church is discussed. In September the topic will be the Feast of Trumpets, which is indicated on the Enoch calendar to be special this year. The author will be celebrating that feast on Fri 20 Sep 2002 in Orem, Utah.

Let us begin by considering how the Hebrew calendar indicates a meridian of time, and then discuss the newly discovered witness of the Enoch calendar. It should be noted that the relationship of this meridian to the 7,000-year temporal history of the earth is not discussed,[1] but rather the meridian as indicated on these two calendars.

1. The Day-Year Pattern

The Lord has told us that he counts years the same way as days. For example, he had the children of Israel consigned to the wilderness for forty years, based on their searching out of the land for forty days. He explicitly stated the he reckoned "each day for a year" (Num. 14:34). Similarly, he had the prophet Ezekiel perform a symbolic act for a specified number of days. The Lord explained, "I have appointed thee each day for a year" (Ezek. 4:6). These verses suggest that the Lord might use a calendar in which he numbers the years in the same way that he instructed us to number days. The 7-year sabbatical cycle supports this interpretation. Counting years as days can be called the "day-year pattern".

The Sabbatical Cycle. The Lord told Moses to count years by sevens, even as days are counted by sevens. Years of the sabbath cycle of 7 years begin in the fall, rather than the spring. Detailed instructions were given as to how to celebrate every seventh year, which was designed to be a year of release, free from work and the cares of the world, even as the weekly sabbath day is a day of rest (Lev. 25).[2] Traditionally sabbath years can be found as being the Hebrew years that are exactly divisible by seven. For example, the year 2001 was the Hebrew year 5761, which began the previous fall on Sat 30 Sep 2000. The number 5,761 is evenly divisible by 7, so that year was the sabbath year which completed a "week" of seven years. All of my calculations agree that the Hebrew tradition is correct. An easy way to remember where we are currently in the sabbatical cycle is that the destruction of the Twin Towers on 11 Sep 2001 occurred in the last weeks of a seven-year period.

It is convenient to label years of the sabbatical cycle as SUNDAY, MONDAY, etc., the same as we do days of the week, so that the sabbath year would be called SATURDAY, the last year of a week of years. The name in all capital letters means that a year is indicated rather than a day. Thus, this year is a SUNDAY, the first year of the 7-year cycle.

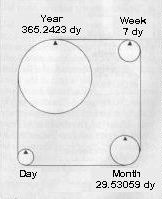
The Hebrew Calendar. The Hebrew calendar has every month start near a new moon. Because twelve moons ("months") require only about 354 days, sometimes an entire extra month of 30 days is added so that the year averages 365.24 days. The details of this mechanism are not needed here. It is only necessary to understand that the calendar has a precise formula for chaining together years of six different lengths: 353, 354, 355, 383, 384, or 385 days. Each type of year can only begin on certain days of the week, and they follow a set pattern.

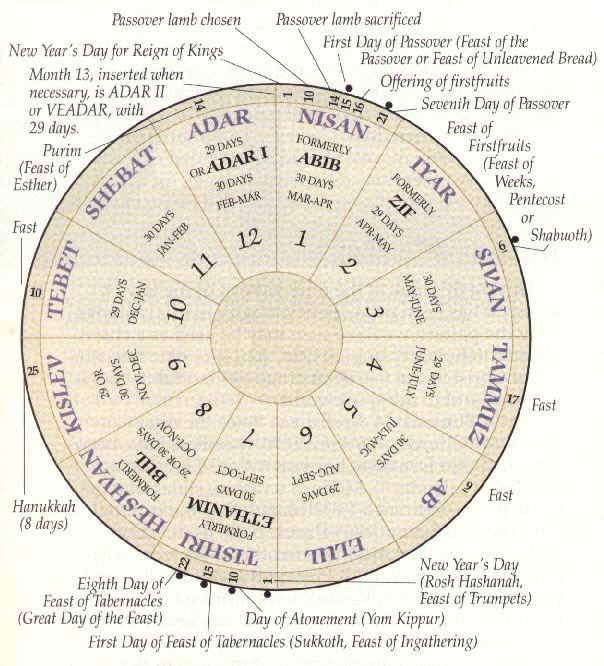
The Hebrew calendar is shown in Figure 1. It has twelve months, with a thirteenth month called Adar 2 added seven times every nineteen years. Most of the feast days are indicated, except that Moses was also told that the first day of every month was also a sacred day. There are two different "New Year's Days" on this calendar. The day 1 Nisan is the first day of the first month, and the beginning of the year for king's reigns and other purposes. The day 1 Tishri is the first day of the seventh month. It begins the year when counting the sabbatical cycle, and it is used by modern Hebrews as the beginning of the civil year.

Figure 1. The Hebrew Calendar

Great Years. Let us now attempt to use the same pattern employed in naming and numbering days of the Hebrew calendar to naming and numbering years. To my knowledge this has not been done before. I believe I have been successful in fitting the Hebrew calendar template over the years and there is exactly one way that fits perfectly throughout history. It is not my purpose now to publish all those details here, but it suffices to say that there is such a strikingly meaningful symbolism throughout history to make a strong case both that God actually is using the pattern and that he knows the end from the beginning.

The idea then, is to name some year 1 NISAN, and then the following year 2 NISAN, and so on, following the Hebrew calendar pattern. Capital letters will be used to indicate that 1 NISAN refers to an entire year. This numbering of years refers to years which begin on the day 1 Nisan in the spring. On the other hand, the naming of years for the days of the week, which corresponds to the sabbatical cycle, refers to years which begin on 1 Tishri in the autumn. Thus, a SATURDAY year begins in the fall. This is complicated, but it is how the system appears to work. One last needed detail is that the patterns of the six different possible year lengths refer only to years beginning on 1 Tishri.

Let us define a "Great Year" to be the set of years either from a year 1 NISAN to 1 NISAN or from a year 1 TISHRI to the next 1 TISHRI. Thus, a Great Year may comprise 353, 354, 355, 383, 384, or 385 years, each being referred to as if it were a day on the Hebrew calendar.

The Chosen Fit. So how do we go about fitting the template of the Hebrew calendar cycle to map a year to a day? The details of this mapping have not yet been published, nor even the template of the Perpetual Hebrew Calendar, which is the corrected version used in my articles. All that is needed to know for this article is that the pattern is a fixed pattern throughout all of history, and that it only has to be correlated to one day in history in order to be defined for every day.

Passover is the designated feast on the Hebrew calendar which symbolizes the first coming of Christ in the meridian of time.[3] Christ was born, began his ministry, and died at Passover. Thus, an obvious choice is to align the Hebrew day-year template so that one of those three years corresponded to the year 15 NISAN. That way, the event would have occurred on the day 15 Nisan of the year 15 NISAN. The choice which results in many key events of history having occurred in "holy years" is to choose the beginning of the Savior's public ministry, Sat 6 Apr AD 30, to have been in a year 15 NISAN. It must be emphasized that once that date is fixed to a point in the template, all years in history are determined; no other choices can be made. While an entire chronology of history is beyond the scope of this article, it seems like one example is in order to show the power of the symbolism of Great Years.

The Babylonian Captivity. The Lord prophesied through Jeremiah that there would be a seventy-year period when Judah would be taken captive to Babylon (Jer. 25:11). Let us construct a Great Year mapping which covers that time period, counting back from setting the year AD 30 to be 15 Nisan. The following table summarizes the anchor points, where WEEKDAY refers to the year of the sabbatical cycle, which began the previous autumn, and DAY refers to the Hebrew year beginning in the spring of that year.

YearWEEKDAYDAYGreat Year Length
-899THURSDAY1 TISHRI354 years
-545MONDAY1 TISHRI353 years
-192THURSDAY1 TISHRI385 years
193THURSDAY1 TISHRI354 years

In this table, the astronomical method of listing years is used where the positive years mean AD, and the negative years differ by one from BC years. That is, the year -192 refers to 193 BC. Astronomers prefer this method because it shows the true numerical relationships. The BC method suffers from having no 0 BC year between AD 1 and 1 BC. For example, the number of years separating -192 and 193 can be easily calculated to be 385 years.

Three of the major dates associated with the Babylonian captivity are: 1) when Daniel and the first captives were taken in the first of the seventy years, 2) when the king and most of the city were taken, and 3) when they were released and celebrated at the feast of tabernacles in Jerusalem in the seventieth year.[4] When the years are counted the same as days, starting from 1 TISHRI in -899 (900 BC), a very clear pattern emerges:

EventGregorian CalendarPerpetual Hebrew Calendar
Daniel taken captiveSat 18 Jun 605 BC pm*Sun 17 Tammuz FRI 1 AB
King Jeconiah captiveSat 10 Mar 597 BCSat 1 Nisan SAT 9 AB
Feast of TabernaclesSun 11 Sep 537 BC pm*Mon 15 Tishri THU 10 TISHRI

The notation am* and pm* refers to before 6 a.m. and after 6 p.m., respectively, when the stars (*'s) are shining. The meaning of the seventy years now becomes significant when seen in the light of counting the years the same as days. The years of the sabbatical cycle are indicated as FRI, SAT, and THU and the day/month years are shown as 1 AB, 9 AB, and 10 TISHRI.

What will be obvious to those familiar with the Hebrew calendar is that 1 AB, 9 AB, and 10 TISHRI are all days designated as holy days on the hebrew calendar (See Figure 1). The day 1 AB is the least significant, being the first day of the month Ab, and a minor holy day as was the first day of every month. The second day, 9 Ab, is an annual fast day commemorating the destruction of the temple both in 587 BC and again in AD 70. The day 10 Tishri is the Day of Atonement, the holiest day of the year, being a day for reconciliation with God. Thus, the years marking the 70-year captivity are not only all "holy years," each is also significant in itself: a year of beginning, a year of mourning, and a year of reconciliation with God. It is these significant patterns which suggest that God actually uses this day-year reckoning.

Christ born at Meridian of Great Year. Following the same pattern shows that 6 Apr 1 BC fell in the year called 14 ADAR 2. The Feast of Esther begins on the day 14 Adar, or, in years with the thirteenth month, on 14 Adar2. So the proposed year of the Savior's birth also fell in a "holy year" of the Great Year, corresponding to the Feast of Esther.

Moreover, that particular Great Year comprised 385 years. The Feast of Esther that year fell in the 193rd year of the Great Year, which is precisely the middle year of the 385 years. So the birth year of Christ occurred at the meridian of a Great Year, which was also a "holy year."

One final point: the name Esther means "A star," so the birth year of Christ was the year of the "Feast of A Star." That seems appropriate, in light of the appearance of the Star of Bethlehem, which heralded his coming. If that was planned, then even Esther's very name was inspired.

Christ born at Meridian of Jubilee Year. The year beginning in Sep., 2 BC was a SUNDAY, the first year of the sabbatical cycle. In fact, it was also a Jubilee year which is always a SUNDAY, occuring every 49 years.[5] The jubilee year was to be announced with the blowing of the trumpet on the Day of Atonement (in September/October) (Lev. 25:9-10). If Christ was born during the night preceding 6 Apr 1 BC, as all of my calculations indicate, then he was born exactly on the meridian day of that Jubilee year, which was also the day of Passover. That is, from 10 Tishri to 15 Nisan is half a solar year. A normal Hebrew year is ten days short of a solar year, to the 5 extra days from the 10th to the 15th is exactly what is required to separate the two days by half a solar year. Thus, the meridian of time is precise down to the very day, not just the year. Now let us turn to another witness of the meridian of time.

2. The Enoch Calendar

In a previous article[6] we have discussed the fact that the Book of Enoch used to be in the Bible and was accepted by the Savior and his apostles as having been written by the antediluvian prophet Enoch, so I will refer to it as if actually written by Enoch. We noted that it describes a calendar, but that it was sketchy on the details of just how to add the extra weeks to its 364-day year in order to keep it aligned with the seasons.

The reader's indulgence is asked in reading through the following overview of how the Enoch calendar works. Only a brief description and a bare minimum of mathematics will be included, needed to appreciate just how precise the meridian of time really is.

Figure 2. The Enoch Calendar

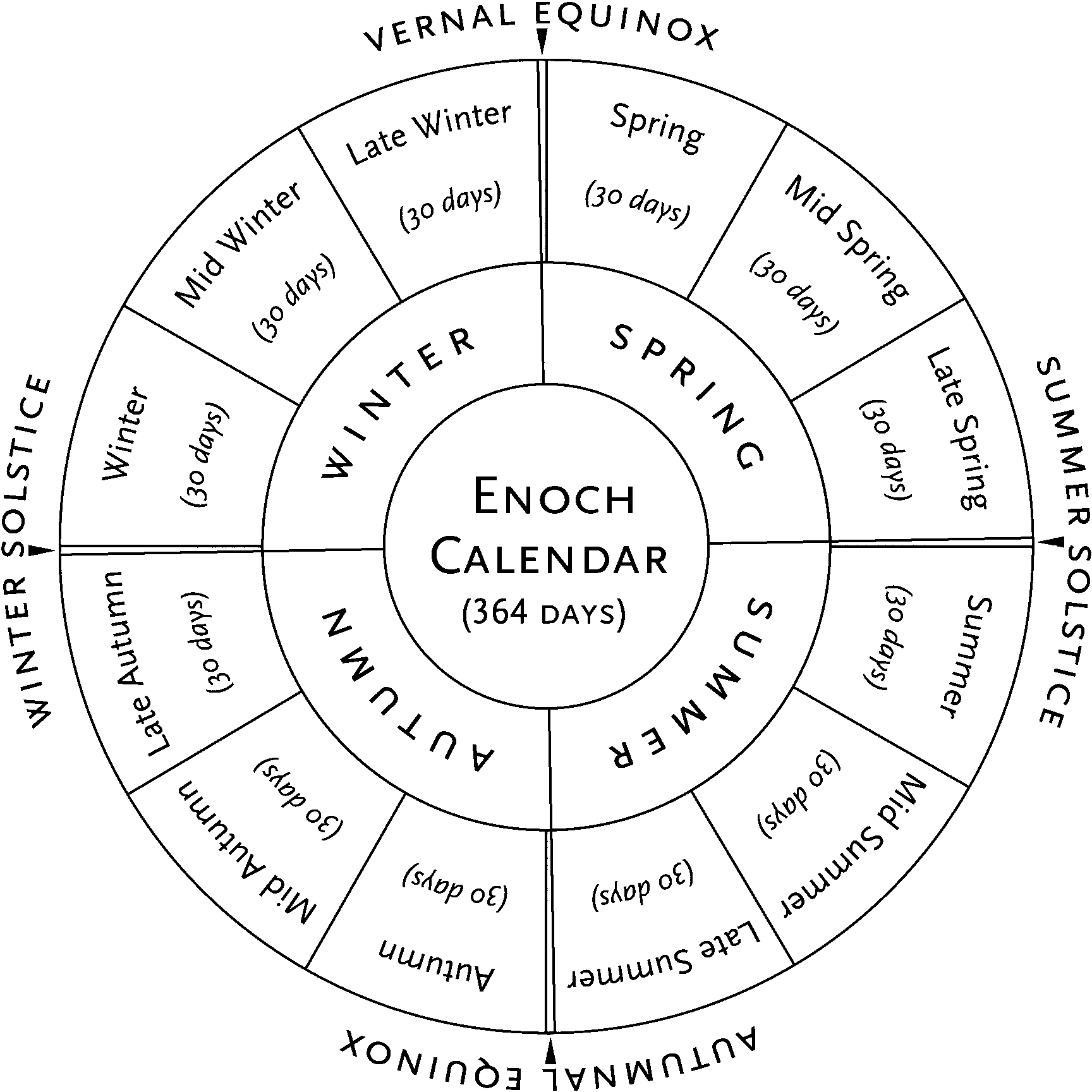Aligned with New Moon. The Enoch calendar has 364-day years, each comprising four 91-day quarters and exactly 52 weeks (See Figure 2). The year begins in the spring, on a Sunday near the first day of spring on 20-21 March on our calendar. For example, this year it begins on Sunday, 24 Mar 2002. Because the Enoch year has only 364 days, it begins a day earlier every year according to our 365-day calendar. Thus, next year it will begin on Sun 23 Mar 2003. Every few years an entire extra week of seven days is added, so that the first day is always on a Sunday near the spring equinox, when the sun rises due east and appears to enter the northern part of the sky.

The Problem. The big problem which Enoch leaves as an exercise for the reader is just when to add the extra week. Fortunately, Enoch provides the clue needed. He states that the year should also begin near a new moon if possible (Enoch 73:13-14, 12, 16). At first blush that sounds like a tall order, because it might turn out that just when we need to add a week to keep the year beginning at the right season, that the new starting day would fall on a full moon. So how can we be sure that we can always avoid a full moon occurring on the indicated Sunday near the first day of spring?

The Solution. Without going through the derivation, let's just look at the answer. A calendar is a device to replace complicated mathematical calculations with a simple pattern that gives the same result. It turns out that one can use a pattern of adding five extra weeks every 27 years to avoid having the Enoch year start within a day of a full moon all through history.[7] To see how that works, we need to understand realignment cycles.

3. Realignment Cycles

Figure 3. The hands of a clock realign on twelve every twelve hours.
Both the Enoch calendar and the Hebrew calendar realign three cycles, namely the week of seven days, the lunar month of 29.530594 days and the year of 365.2423 days.[8] It is like approximately lining up hands on a clock where the cycles were not simple multiples of each other. In other words, the hands on our clocks line up perfectly twice a day because there are exactly 24 hours in one day (See Figure 3). The hands on a clock using the cycles of the week, lunar month and solar year would never line up perfectly, but over increasingly long intervals, they would line up better and better (See Figure 4).[9]

Figure 4. The Hebrew and Enoch calendars align the week, month and year.
It is easy to have a computer calculate just what are the intervals of time which approximately make these intervals "come out even." Those intervals "realign" the cycles, much like the hands on a clock are realigned at midnight and noon. Periods which align all the cycles better than any shorter period are called "realignment cycles." Calculations show that realignment cycles for the week, month and year include 3, 11, 27, 57, 68, 152, 220, 372, 1,803, 2,023 and 3,454 years.[10] That means that after those numbers of years, that the Enoch and Hebrew calendars will approximately begin to repeat. The longer intervals give the best alignments.

4. Enoch Calendar Realignments

In order to define how the Enoch calendar might work, it is only necessary to derive a simple method of using realignment cycles, so that the Enoch calendar can be determined throughout history. The 27-year cycle mentioned above is one of those intervals. If we were to simply use that table by cycling around it forever, then with each 27-year period, the error would accumulate to become unacceptably large. But it turns out that we can count first 68 years and then 84 years around the 27-year table to achieve the greater accuracy of the 152 year realignment cycle. Then another 68-year period brings the even greater accuracy of the 220-year realignment cycle. Similarly, the counts can be extended to finally reach the 3,454-year realignment cycle, it being the most accurate. There may be more accurate cycles larger than this, but this is the best we can calculate using the orbital accuracies known today.

5. Witness of the Enoch Calendar

So what has all on this got to do with a witness about the meridian of time? Your patience in dealing with these tedious numbers is about to pay off. Having determined the realignment intervals and how to use the 27-year table, we now need only determine when the moon happens to be in the right position to know precisely when to begin the table. The table begins with four consecutive 364-day years, so it needs to start on a day about 23 March, so that the first four years will begin on 23 March, 22 March, 21 March, and 20 March.[11] The Enoch calendar always begins on a Sunday, so it is only necessary to find the Sun 23 Mar days throughout history which are at a new moon.

Before looking at the table of results, allow me to remind you what to expect. We can have the computer search for dates with a new moon. After the first is found, the others will be found separated by realignment cycles. Such dates usually appear to be very random, and one would have to look carefully to notice the realignment interval patterns.

Now let us look at the results. It turns out that if we search from 4000 BC to AD 4000 for Sun 23 Mar with the moon's mean phase at 0.0 days, that not one day in history is found to meet those criteria! If we instead seek for the phase 0.1 days, then the following dates are found:[12]

DateLunar Phase (days)
Sun 23 Mar -39970.1
Sun 23 Mar -31580.1
Sun 23 Mar -25660.1
Sun 23 Mar -23190.1
Sun 23 Mar -17270.1
Sun 23 Mar -2960.1
Sun 22 Mar 2960.1
Sun 23 Mar 17270.1
Sun 23 Mar 23190.1
Sun 23 Mar 25660.1
Sun 23 Mar 31580.1
Sun 23 Mar 39970.1
What is supposed to jump out at you in this list is that every negative year has a positive year counterpart (again, astronomical notation of years is used). That is totally unexpected and very significant.

Meridian of Time. Coming back to the concept of the meridian of time, we see that all of the dates are spaced equally around the astronomical year 0, which historians call 1 BC. Indeed it appears that the entire table was designed to emphasize the symmetry around that year. The key lines in this table are those for -1727 and +1727. They are separated by exactly 3,454 years, which was the most accurate realignment cycle found. The amazing coincidence which causes the table's symmetry is that a 3,454 year alignment period just happens to be centered exactly on the year 0. That seems unusual enough as to constitute evidence for celestial planning on the part of the Creator. But the symmetry continues if we look with a higher power microscope.

My model of the Enoch calendar pieces together chains of 68- and 84-year cycles to make ever more accurate chains. In particular, starting in the year -296, one counts to the year +296 with chains of 220, 152, and 220 years, each of which is a realignment cycle. Alternating the lengths is important because one is too long and the other too short, so that will maximize accuracy for every year while building increasingly accurate longer pieces. Each 220 years is counted as 68-84-68, and the 152 as 68-84. That means that the table in detail around the year 0 (1 BC) looks as follows:

DateCountLunar Phase (days)
Sun 23 Mar -296start 68 (also 220, 592)0.1
Sun 22 Mar -228start 840.9
Sun 23 Mar -144start 68-0.4
Sun 23 Mar -76start 68 (start 152)0.4
Sun 22 Mar -8start 841.1
Sun 23 Mar 8continue 84-0.9
Sun 22 Mar 76start 68 (start 220)-0.1
Sun 22 Mar 144start 840.6
Sun 23 Mar 228start 68-0.7
Sun 22 Mar 296start 68 (start 1431)0.1

The point of this detail is that the seemingly random-looking periods of counting 68 and 84 years needed to create the longer chains of 152 and 220 years also form a pattern which is exactly centered on the year zero. So even the length of the shorter chains work together to form a perfect symmetry which emphasizes the crossover point at the year 0. To me, this is very strong evidence that orbits of the earth and moon were carefully aligned at the Creation to be centered on Christ's birth at the meridian of time. Looking at it from the laws of physics, I would say that the Creator set the "initial conditions" to be exactly as he wished. Thus, the Enoch calendar bears testimony that the meridian of time occurred in the year 0 (1 BC).

6. Conclusion

Scientists have found a high degree of order in the motion of the planets in the solar system, which they explain with natural laws. That is fine as far as it goes, but they have assumed that the precise orbital periods, such as 29.53059 days for the mean period of the moon's phases, were simply random numbers, resulting from a Big Bang explosion long ago. Books with titles like The Blind Watchmaker have been written to ridicule the idea that God created the heavens to be a precise timepiece. Such groundless diatribe will not withstand the test of time.

If Alma were to refute the agnostic Korihor today with his testimony that "all the planets which move in their regular form do witness that there is a Supreme Creator" (Alma 30:44), Korihor would answer that natural laws have explained everything. But given the more precise alignments such as those in this article which depend on the exact values of the orbital periods, Korihor would be stumped. There are no known natural laws to explain the precise values of orbital periods; they are simply assumed to be random, referred to in physics as "initial conditions." He would be unable to muster any refutation except that all the known alignments are merely lucky coincidences. That rebuttal is so unlikely to be true that it is ludicrous. Thus, even today, Korihor should remain mute.

The results summarized in this article indicate that the solar system does indeed constitute an incredibly accurate clock which not only chronicles events perfectly throughout history, but also implies that key events were known ahead of time by the Lord. We should not be surprised because he has told us all along that he knows the end from the beginning. Truly, the Lord meant it literally when he stated that "all things are created and made to bear record of me" (Moses 6:63). The heavens brilliantly declare the glory of God and testify irrefutably that there is a Supreme Creator.

Notes

  1. The 7,000 years are apparently treated as 7 days of 1,000 years each, and indivisible as far as the meridian of time is concerned. The meridian occurs between the fourth and fifth day on that calendar.
  2. See Millett, Ronald P., "A Year's Supply for Times of Liberty and Plenty," Meridian Magazine, 8 Apr 2002.
  3. See Pratt, J.P.,"Passover: Was it Symbolic of His Coming?" The Ensign 24, 1 (Jan, 1994), pp 38-45 (section 3).
  4. The seventy years were counted from 1 Tishri. See Pratt, J.P., "When Was Judah's 70-Year Babylonian Captivity?" The Ensign 28, No. 10 (October, 1998), pp. 64-65.
  5. I have not published a derivation of the jubilee year, and it is currently not generally known to scholars, but I couldn't pass up including it here to show that the very day of Christ's birth was the meridian of time. The jubilee is the fiftieth year of the sabbatical cycle, and is counted inclusively as the first year of the next jubilee cycle. Thus, although it is the fiftieth year of the cycle, the cycle only contains 49 years. The day-year pattern also obtains here because the Feast of Firstfruits is counted exactly the same. It occurs "fifty days" after the sheaf offering, which was exactly 7 weeks thereafter (Lev. 23:15-16). The Sadducee sect of Judaism interpreted that to mean that both offerings always occurred on a Sunday, which appears to me to be correct.
  6. Pratt, J.P., "Enoch Calendar Testifies of Christ", Meridian Magazine (11 Sep 2001), section 1.
  7. The pattern is that the 5th, 7th, 16th, 21st, and 23rd years of the 27 have 371 days. The rest each have 364 days.
  8. That value for the lunar month is so accurate that it can be used throughout history. It is the value used in the traditional Hebrew calendar. The modern astronomical estimate is slightly different, being 29.5305956 days, being the average from 4,000 BC to AD 3,000. The length of the year is slowly changing. It is currently equal to 365.2422 days, but somewhere between 365.2423 to 365.2425 days is a better average throughout history, depending how far into the future one wishes to project. The Lord seems to use the 365.2423 days, so I do too.
  9. See "Realignment Intervals" section of "The Symbolism of Passover and of Elijah's Return" Ensign 15, No. 7 (July, 1985), pp. 55-64 for more on Realignment intervals.
  10. These can be calculated on my web site at http://www.johnpratt.com/items/calendar/mathutil/realign.html . For reference, here is a table, which includes the realignment intervals, and some close hits:
    YearsMonthsWeeYear ErrorMonth Error
    337156-3.727-0.632
    11136574+0.335+1.839
    273341,409+1.458-0.218
    577052,974-0.811-1.069
    688413,548-0.476+0.770
    841,0394,383+0.647-1.287
    1521,8807,931+0.170-0.517
    2202,72111,479-0.306+0.258
    3724,60119,410-0.136-0.263
    5927,32230,889-0.442-0.009
    83910,37743,777+0.710+0.026
    1,43117,69974,666+0.269+0.017
    1,80322,30094,076+0.133-0.246
    2,02325,021105,555-0.173+0.008
    3,45442,720180,2210.096+0.024

  11. It is desirable to have the years start after the first day of spring because then the fall equinox will also be close to the true value. The true fall equinox is about 23 Sep, so in years when the fall equinox on the Enoch calendar falls on Sat 23 Sep, the spring must fall on Sat 25 Mar.
  12. These calculations can be verified with the calendrical conversions on my web site at http://www.johnpratt.com/items/calendar/calcalc/calcalc.html, by choosing the "Planets" calendar and leaving it on the default version, which is the moon. Simply enter the date into a Gregorian calendar and the lunar phase in days will appear in the Planets calendar. They can also be repeated by a) calculating the day = Julian Day - 9.70, then the phase = period*FRAC(day/period) where period = 29.5305956. For example, Sun 23 Mar 1727 is Julian Day 2,351,915, yielding a phase of 0.075, which rounds up to 0.1. Note that the only exception in the table is that in AD 296 the day falls on 22 Mar instead of 23. That has to do with the precise manner in which leap days are inserted into our own Gregorian calendar. It turns out that 22 Mar 296 dates is the only Sun 22 Mar from AD 1 to 4000 that has a lunar phase of 0.1 days, so it is included in the list.