Perhaps the greatest contribution to astronomy from ancient Chaldea was the discovery of a period of 6,585 days (18.03 years) called the saros, after which eclipses might repeat.*
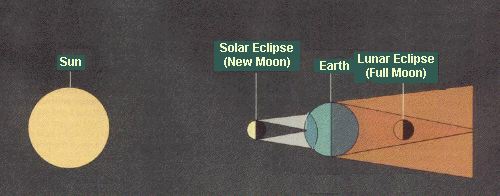
An eclipse occurs when the sun, moon, and earth form a straight line. Solar eclipses occur at a new moon, when the earth is in the moon's shadow; lunar eclipses are at full moon, when the moon passes into the earth's shadow. (See Figure 1.)
 |
 |
1. The phase (full or new) of the moon must be the same, which is why similar eclipses are always separated by a whole number of lunar months of 29.53059 days.
2. The moon must be near the place where its path crosses the sun's apparent path. The period of such crossings is 27.21222 days.
3. The moon needs to be at about the same distance from the earth in order to completely cover the sun in total solar eclipses. (The moon's distance from the earth changes because its orbit is not circular, which makes its apparent size vary by about 10 percent.) This reoccurs in intervals of 27.55455 days.
Thus, the problem of predicting when eclipses will repeat is a question of finding a realignment interval for those three cycles. (See Figure 2.) After an eclipse, when will all three cycles again coincide? One of the very best realignment intervals is the saros of 6,585.32 days.
As discussed in the text, the return of Elijah occurred 100 saros periods after the proposed date of the Savior's resurrection.
*Arthur Berry, A Short History of Astronomy (New York: Dover, 1961), p. 19. The Babylonians are known to have been aware of the saros since at least several centuries B.C. It is not known whether such knowledge dates back to the time of Abraham, who lived in that same area about 2000 B.C.