Enoch and Star Calendar Leap Years

by John P. Pratt
24 Mar 2019, New Year (E), 1 Serpent (SR), 1 Aqr (US), Easter (PH, M)

©2019 by John P. Pratt. All rights Reserved.

Index, Home

Contents

1. Intercalation Principles 1.1 Patterns for Predictability 1.2 Long Term Accuracy 1.3 Simple and Elegant 1.4 Day Count Foundation 1.5 Nested Patterns 1.6 Snap to Grid 1.7 Serving Two Masters 1.8 One Year With God 2. Enoch Calendar 2.1 Intercalation Scheme 2.2 Starting Point 3. Star Calendar 3.1 Intercalation Scheme 3.2 Starting Point 4. Conclusion Notes

Sacred calendar leap year principles are reviewed and applied to the Enoch and Star Calendars.

Methods of inserting leap days ("intercalation") into years to achieve long term accuracy are the trade secrets of sacred calendars. These techniques are often omitted entirely from scriptural calendar descriptions, including even the calendar to be used to celebrate holy days in the law of Moses. The same is true of my work, where intercalation rules are buried in footnotes or omitted entirely because they have not been well understood.

Equinox sunrise through Yucatan temple.

This article summarizes intercalation principles both for all calendars as well as for the special case of God's sacred calendars which have been discovered in my work. It then applies those principles to the very important Enoch Calendar (E), which is a companion to the Hebrew Calendar. It then proposes that the intercalation method used in the recently discovered Star Calendar (S) is nearly identical as that of the Enoch Calendar.

This article discusses technical intercalation details which are most likely not of interest to readers who desire only a basic understanding of sacred calendars.

This section summarizes both intercalation principles which can be applied to all calendars as well as special techniques which have been discovered as used in the Lord's sacred calendars. The first five subsections below are principles for all calendars which were proposed in an earlier article to be the basis of a 5-star calendar rating system.[1] The last three subsections apply mostly to the sacred calendars.

1.1 Patterns for Predictability

One of the main functions of a calendar is to enable the scheduling of future events. Indeed, one definition of the word "calendar" today is a verb meaning "to schedule". If future dates depend on observations yet to be made, then one cannot plan with any precision.

Such a calendar should be entirely predictable, reproducible solely by mathematical calculations or tables without any reference to actual observations of the sky. Of course, astronomers should have first made their most accurate, precise observations of the cycles that the calendar is designed to track. The whole idea of a calendar, however, is to replace observations, preferably with simple patterns. For example, the pattern of a year replaces the need to go make annual observations of just when the year begins and the pattern of a 7-day week may tell us the appropriate time to worship.

1.2 Long Term Accuracy

Another important feature of a calendar is that it not slowly drift away from whatever celestial body it is tracking. Ensuring long-term accuracy is a principal reason that some calendars require continual observations.

Calendar reform usually is a mechanism to improve long-term accuracy. The "Old Style" Julian calendar, which had a leap year every four years in order to make years average 365.25 days, was replaced with our modern Gregorian calendar when it was discovered that the year is really only about 365.2422 days long. By skipping leap years in three out of four century years, the Gregorian calendar averages 365.2425 days per year, a much better approximation.

1.3 Simple and Elegant

Equally important as long-term accuracy, and much more important than short term accuracy, is the need for a calendar to have a simple repeating pattern. An extremely accurate calendar might be so complicated that the layman would not be able to understand it. On the other hand, if one clings exclusively to a very simple pattern, which might be only a crude approximation, then the calendar will probably suffer long term drift. This is a classic case where art and science meet; the best calendars strike a balance between simplicity and accuracy.

For example, the Julian calendar, which has a leap year every four years, certainly has a simple pattern, but that requirement for simplicity is less important when correcting for long term drift. The Gregorian calendar skips the leap day in three out of every four centuries, which is an excellent way to correct the problem without detracting from the overall simplicity of the calendar.

An example of good long term accuracy with a poor pattern is the following possible correction to the Julian calendar. Inserting one extra year after every eighth leap year creates blocks of 33 years which contain 8 leap days, leading to an average year length of (33×365 + 8)/33 = 365.2424 days, which rivals the Gregorian approximation for accuracy. The price of that increased accuracy, however, is the loss of the simple rule of dividing a year by four to know if it is a leap year.

Another example of a good balance between simplicity and accuracy is the Jubilee Calendar intercalation. That calendar groups years by sevens into jubilees of 49 years. The leap years are the same years in every jubilee, usually in a FRIDAY year and never in a SATURDAY or SUNDAY year. That is not a simple as every fourth year, but it is more accurate and matches the jubilee pattern.

1.4 Day Count Foundation

One feature of advanced calendars is an uninterrupted day count that is aligned with other cycles. A day count provides a double check on any given date and on long term calculations, especially for calendars which are not perfectly predictable. An example of an uninterrupted day count is the 7-day week; it was not broken even during the transition from the Julian to the Gregorian calendar. It has been an uninterrupted cycle since at least the sixth century BC. If one includes the day of the week with the date, then that redundant information serves as a double check to verify accuracy. When the date of an upcoming event includes the weekday, that is often more important in planning than is knowing the exact date.

1.5 Nested Patterns

Perhaps the most advanced feature of certain calendars is the use of nested cycles or "wheels within wheels". The best method is to use the very same pattern to reckon increasingly larger cycles of time, which usually are not linked to any physical phenomena. The most common use of nested cycles is to count years in the same way as days. For example, the Hebrews count days by sevens and also count years by sevens. Moreover, there is one especially holy year which was to be reckoned, according to the law of Moses, in exactly the same manner as one especially holy day: the jubilee year was the fiftieth year and the feast of Pentecost was the fiftieth day.

1.6 Snap to Grid

Randomly placed icons "snap to grid" to be in orderly rows and columns.

Now we come to advanced calendar features which are used in the sacred calendars of God. The first is similar to the "snap to grid" concept developed for modern computers. Instead of having icons spread at random all over a computer screen, it is usually more pleasing to have them all aligned in neat rows. If an icon is placed randomly on the screen, it automatically is adjusted to fit neatly into a row and column.

The same concept is used in sacred calendars to adjust the position of celestial events to the nearest holy day "grid" position. For example, the spring equinox, when the apparent position of the sun crossed into the northern part of the sky, occurred this year on Wed 20 Mar 2019. On the Enoch Calendar, the Spring Equinox is a holy day which always occurs on a Saturday, usually on or after the actual equinox. This year Spring Equinox (E) was on Sat 23 Mar 2019. Thus, it "snaps" or "jumps" to the nearest Saturday (grid) day afterward.

Sometimes this snapping can be more significant. Consider how Easter is celebrated each year. The pattern desired to mimic the actual resurrection of Christ is that Easter should be on the first Sunday after the first full moon on or after the spring equinox. In order to avoid the details of observing the actual full moon every year and to make the holy day predictable, an approximating equation is used for the lunar phase. Moreover, to avoid problems of the exact moment when the spring equinox occurs, which could be before midnight in one country and after midnight in another and hence on different days, the equinox snaps to the grid day of 21 March. This year the first full moon after Thu 21 Mar is on Fri 19 Apr and Easter will be on Sun 21 Apr 2019. On the Perpetual Hebrew Calendar (PH), however, Easter is today, Sun 24 Mar 2019. That calendar also calculates the same pattern and yet the results differ by almost a month.

When did the actual events happen? This year the full moon occurred about three hours after the spring equinox on Wed 20 Mar in the United States, so indeed Sun 24 Mar is the first Sunday afterward. Thus, Easter snaps not only to the grid of being on a Sunday but also to dates of both equinox and full moon.

Another aspect of the "snap to grid" concept is important in sacred calendars: it is desirable to have holy days on different sacred calendars coincide when practical. That allows a story to be told about a sacred event if it occurs on multiple holy days. For example, the day on which Jesus was baptized was Atonement (PH), the day to be reconciled with God. It was 0 Prime (Rebirth) on the Venus Calendar, the day for spiritual rebirth which is represented by baptism. It was also 13 Water on the Sacred Round, the day to be spiritually cleansed by a ritual washing away of sins. It was also the star day "Redeemed" (S). Thus, together they tell the story, which was made possible because all of those holy days snap to a grid that helped them coincide.

1.7 Serving Two Masters

It's hard to serve two masters.

Now we come to a principle which is the key to the Enoch Calendar intercalation. Every scholarly paper known to me describes the Enoch Calendar as a solar calendar. That means it is designed to track only the sun. In particular, it is designed to align the first day of its year to occur on or after the spring equinox.

The first day of the Enoch Calendar year snaps to the grid of the week. The Book of Enoch does not specify on which weekday it begins, but emphasizes that it must always have 364 days, which is exactly 52 weeks. The Essenes at the time of Christ chose Wednesday to be the first day of the year on the Qumran calendar because the sun first appeared on the fourth day of creation (Gen. 1:16,19) and Wednesday is the fourth day of the week. The implementation which God appears to using, however, has New Year's Day (E) always occur on a Sunday, so that is the version used in my work.

One can usually identify the day of the spring equinox by simply sighting the sunrise over a pointer which is due east. Egyptian temples sometimes had a long corridor facing due east so that on the equinox day, it would light up a wall at the inner end of the hallway. The sun's apparent motion along the equator is most rapid at the equinox, moving more than one entire solar diameter per day. Thus, it usually is easy to determine the date of the spring equinox by observation.

But what about cases where the sun rises equally south of east on Sun 20 Mar and equally north of east on the next day? How are tied results to be scored? There needs to be a tie breaker condition.

The Book of Enoch actually provides the answer to this question, but it has been almost entirely overlooked. Enoch states,

"The moon brings on all the years exactly, that their stations may come neither too forwards nor too backwards a single day; but that the years may be changed with correct precision in 364 days." -- Enoch 73:13.

That enigmatic verse has been ignored by scholars because it is not at all clear what it means. How can the moon bring in solar years, which are governed by the sun. Can a calendar server two masters, both the sun and the moon? If those two masters agree then it is easy, but when they do not, only one can be obeyed (Matt. 6:24). Is it possible to compromise by not fully obeying either one but doing the best to satisfy both?

Before solving that riddle, let us consider why one would want to involve the moon at all in a solar calendar. The answer was discussed in the Snap to Grid section. It is desirous to have the holy days on different sacred calendars coincide as much as possible. The choice of exactly when to intercalate the Enoch Calendar provides an opportunity for that calendar to share more holy days with the Perpetual Hebrew Calendar. That calendar is based on the moon, the sun, and week. By allowing the moon to decide close cases, the Enoch Calendar is also based on the sun, week and moon.

1.8 One Year With God

Is annual Jubilee pattern "one year with God"?

Now consider another enigmatic scriptural clue which the Lord has provided in these latter days. Referring to the sun, moon and planets, He has explained that "And they give light to each other in their times and in their seasons, in their minutes, in their hours, in their days, in their weeks, in their months, in their years—all these are one year with God, but not with man (D&C 88:44)." What does it mean that all of the days, weeks, and years of man are one year with God?

Although that scripture may have many meanings, one has been suggested in an earlier article. The Jubilee Calendar divides the year into seven parts with three week-long feasts. They are clearly named to suggest a correlation of the seven millennia of the family of Adam of earth. That is, the Watering represents the Deluge and there is a Burning just before the last Millennium of spirituality (olive oil). Thus, for this calendar, all of the days, weeks, and seasons of the Jubilee Calendar can be seen to use the very same yearly pattern to represent all of our history: "one year with God".

This article will be the first to apply that symbolism to both the Enoch and Star Calendars, as it was only recently discovered to apply more generally to other calendars than the Jubilee. The principal practical use of this concept may be in determining the starting point of each calendar. After the pattern of each calendar is known, it is still necessary to attach the entire pattern to begin on one day of history. Knowing that the pattern corresponds to the approximately 7,200 years from Adam through the "little season" after the Millennium helps to find the correct starting day. That is, knowing that the Jubilee pattern of 7,203 years covers all of history suggests that similar patterns may exist for other sacred calendars and that they would have similar starting and ending times. It is important to keep in mind that all of the calendars were designed by the Creator and hence are highly organized.

Now let us apply these principles to discover the intercalation patterns of the Enoch and Star Calendars.

Table 1. Enoch Calendar Intercalation Cycle.

The Book of Enoch describes in detail a solar calendar of 364 days, called the Enoch Calendar in my work. In order to average 365.242 days, it inserts ("intercalates") entire leap weeks when needed to have the year begin on the first Sunday on or after the spring equinox (usually 20 March) in order to tie the Enoch year to the seasons of the sun. My model of that calendar has been described in an earlier article,[2] including a proposed implementation of Enoch's requirement that intercalation should also have the year begin near a new moon.[3]

2.1 Intercalation Scheme

Observationally, the idea behind intercalation of the Enoch Calendar is that on the last day of every year of 364 days (Sat, Spring Equinox), the sun rises a little farther south than in the former year. When that point reaches due east (true spring equinox) then an extra week should be added to the end of that year so that the sun never rises south of due east on that last day of the year.

The intercalation method stated in the Book of Enoch is not simply to always insert that leap week so that the true equinox occurs on or after a Saturday, but instead to also consider the phase of the moon and when there is a choice between intercalating or not, one should pick the year in which the moon is nearest the new moon phase both before and after the intercalation.

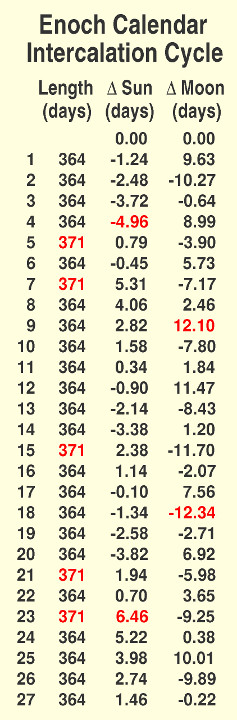
How can that be achieved? Table 1 shows the results of considering both the sun's and moon's average position after every year in a 27-year cycle. That is the number of years required for the sun and moon to both return to very close to their original positions. If the moon were not a factor, then the table could be very simple and result in the Spring Equinox day always falling on a Sat 20 Mar to Sat 26 Mar, a seven day minimum spread of dates. But on some of those dates the moon would be full rather than new. The book of Enoch is saying that it is more important to consider the moon's position too, which results in about a 16-day spread in Equinox dates which spans dates from Sat 16 Mar to Sat 31 Mar.

In the "Length" column of Table 1, the leap years are shown in red as being 371 days long rather than 364 days long. The leap week is the last week of the month Late Winter, just before the Spring Equinox. The earliest solar date of the cycle, as indicated by the date being shown in red in the "Delta Sun" column, is in the fourth year. That column shows how much each year lowers or raises the equinox date from the beginning of the cycle. A common year lowers the solar position by 1.24 days and a leap year raises the date by 5.76 days (-1.24 + 7).

Similarly, the change in the phase of the moon is shown in the next column ("Delta Moon"), with the 0.00 phase at the beginning indicating a new moon. The length of the lunar cycle is 29.53 days. A 364-day year increases the phase by 9.63 days as shown in year 1 of the table, which change can also be thought of as decreasing the phase by 19.90 days (29.53 - 9.63) as shown in that column for year 2. The high and low points of the moon's phase are shown in red in that column, indicating that the new year avoids falling near a full moon (phase 14.77) by at least two days, as desired.

The result of this method confirms that it is indeed hard to serve two masters! The price paid for aligning with the moon so that the Enoch Calendar may coincide more often with the Hebrew Calendar is that the discrepancy between the Spring Equinox holy day from the true equinox day is more than doubled from 7 to 16 days! This demonstrates how important these alignments are between different sacred calendars.

Table 2. Lunisolar realignment intervals.

The last line of Table 1 indicates the days of both the solar and lunar cycles after 27 years. Ideally, if 27 years were a perfect cycle, both of those discrepancies would be exactly 0.00 days as before the cycle started. This is the best cycle to use even though the equinox day ends up 1.46 days later than at the beginning. This has two implications. First, longer periods must be sought which correct these discrepancies even more and second, such periods will require repeating this cycle more than once. A good result of repeating the cycle is that on the second time through, the equinox day will be 1.5 day later and hence begin on Sat 25 Mar or Sat 26 Mar. Thus, the initial 5 day drop will result in an equinox date right on Sat 20 Mar, the true minimum.

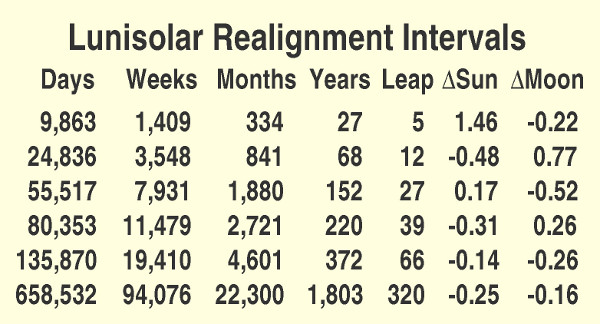Table 2 shows the results of calculating "realignment intervals" after which the three periods of the week (7 days), lunar month (29.53059 days), and solar year (365.2423 days) all realign again better than any other shorter period.[4] They are used by simply counting around the 27-year cycle to get to 68 years and then stopping and starting over at the beginning of the table. Table 2 shows in the "Leap" column that those 68 years require 12 leap years. That means going twice through the table (54 years) gives 10 leap years, so finishing with the first 14 years in the table means those 14 must contain exactly 2 leap years. That is true so that method works. Repeating that process by counting two 68-year cycles plus 16 more to get 152 years means that the first 16 years of the table must have 3 leap years. That is also true, so that works! This method is continued up to 1,803 years. That last period of 1,803 years is important enough in sacred calendars that it was been given the name "saros century" because it is exactly 100 saros eclipse cycle periods of 18.03 years.[5]

2.2 Starting Point

That last section showed that starting on a Sat 23 Mar at a new moon should produce an acceptable intercalation pattern. But how can one know exactly when to begin in order to have the holy days coincide with key sacred events in history? Much time has been spent in my research trying different starting points before the following clue was discovered.

Cycles align when arrows point up.

The Lord has provided a clue in stating that all of history is as one year with God (D&C 88:44). We have seen one interpretation of that scripture above in applying the annual Jubilee Calendar pattern to the 7,200-year history of Adam's family. If so, does it only apply to the Jubilee Calendar?

A few years ago something interesting was noticed about the last entry in Table 2. Four times 1,803 years equals 7,212 years which is very close indeed to the 7,203-year length of history derived from the Jubilee calendar pattern! Moreover, the Enoch Calendar pattern divides the year into four exactly equal seasons even as 7,212 could be thought of as dividing into four seasons of 1,803 years each! Thus, this gives us a clue that the starting point should be shortly before the Beginning of Mortality during the time in the Garden of Eden and then end in the period of the little season after the 7,000-year history. In other words, the Enoch Calendar should also span about the same 7,200 years as does the Jubilee Calendar.

For several years it has been felt that the Enoch Calendar was well understood because such a starting date was found which resulted in the numerous alignments of Enoch holy days with key sacred historical events. That beginning date has been Sat 23 Mar 4055 BC, when the phase of the moon was 0.2 days (0.0 being exactly new).

That starting point is now being investigated again because of possible unforeseen relationships with the Star Calendar, which at this point suggest that this starting date might be improved. As always, this is a work in progress.

The Book of Enoch also mentions a star calendar with 364 days, each represented by a star, which in turn represents a servant of God. Earlier articles introduced the Star Calendar based on that book, laying the groundwork that the year is divided into twelve zodiac "months",[6] identifying all of the stars,[7] placing the stars in order,[8] and identifying the holy days,[9] including the seasonal feast days.[10] It became clear in that last article that the beginning of the Feast Ages, when seasonal feasts are shifted to be in different zodiac constellations, that it is important to know the precise intercalation pattern of inserting leap weeks at the end of the Star Calendar year.

Note: The following intercalation method is no longer used, but is included here for historical purposes because it was used in all Star Calendar calculation to date. It can be skipped by most readers. The method has been superseded by the one proposed in the next article ("Equinox Star Eras", Section 2. "Enoch Calendar Use").

3.1 Intercalation Scheme

What should be the intercalation scheme for the Star Calendar? As a first approximation, only the straight realignment of the stars (sidereal year) with the Enoch year was considered, which is the method which has been used until now. However, after pondering the reasons for which the Enoch Calendar includes lunar phases, it has been realized that there is just as much reason to align the Star Calendar with the Hebrew Calendar as there was for the Enoch Calendar. Thus, let us consider the possibility that the Star Calendar uses an intercalation scheme similar to that of the Enoch Calendar.

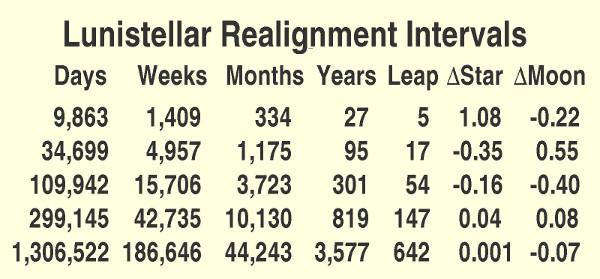
The difference between the sidereal year and the seasonal (tropical) year is very little. The tropical year averages 365.2424 days and the sidereal year is 365.25636 days. That means that the stars shift by 1° every 72 years through the seasons. This small difference means that the 27-year intercalation cycle of the Enoch Calendar (Table 1) can also be used for the sidereal year. In fact, it works even better for the Star Calendar because after one 27-year cycle, the discrepancy is only 1.08 days for the stars instead of 1.46 days for the sun. Of course the discrepancy for the moon is the same for both.

Table 3. Realigning moon with stars.

The longer periods, however, required different longer cycles in order to align. Table 3 shows the longer periods. An excellent short period is 95 years, with the next better period being 301 years. The 95 year cycle can be calculated by simply going around the cycle three times and then cutting off the the fourth cycle after 14 years (3 x 27 + 14 = 95). Doing that leads to the right number of leap years included. After three of those cycles, 301 years can likewise be calculated by cutting off the next cycle after 16 years (3 x 95 + 16 = 301). This time the first 16 years must contain 3 leap years. The 819 year cycle can also be calculated by counting first 301-year cycles and then 95-year cycles in like manner. Similarly, the 3,577 cycle is four 819-year cycles and one 301-year cycle. Note that both the 14 and 16 year requirements are the same for for the lunisolar table. Thus, Table 1 can be used to align both the sun and stars with the moon.

3.2 Starting Point

What about the starting point for the Star Calendar intercalation? Again we can apply the same reasoning as done with the Enoch Calendar. We can see if the intercalation periods might line up with the Star Calendar pattern.

The Star Calendar does not divide into quarters like the Enoch Calendar. Instead, the annual pattern divides into zodiac seasons of varying lengths which depend on the constellation lengths. It was noticed, however, that two of the four royal stars which mark the four main divisions of the sky are exactly 180° away from each other in the zodiac circle. Moreover, when the stars of the calendar were known, it turned out that the year divided exactly in half, with Summer (Uniform Star) starting on 1 Leo (US) exactly half a year away from Winter, starting on 1 Aqr (US). Moreover, the Beginning of Mortality began on 1 Leo (UE), apparently signifying that it was a starting point indeed.

Thus, the Star Calendar year does indeed divide exactly in half, rather than into equal quarters. Looking at Table 3, we see that the longest period is 3,577 years. That could be an excellent length for half of a 7,154-year "year of God" for our entire history of nearly 7,200 years. Thus, it is seen that the proposed interpretation of one year with God may apply to several sacred calendars, including the Star Calendar.

The exact starting point for the beginning of Star Calendar intercalation has yet to be verified, but it was felt that these broad principles were worth publishing even before every detail is known.

Notes