Nebra Sky Disk Depicts Pleiades Rule

by John P. Pratt
27 Jul 2017, 7 Flower (SR)
©2017 by John P. Pratt. All rights Reserved.

Index, Home

Contents

1. Description

1.1 Current Status

1.2 Added Upon

2. Current Interpretations

2.1 General Agreements

2.2 Best Explanation

3. Proposed Interpretation

3.1 Problem: Intercalation

3.2 Solution: Pleiades Rule

3.3 Add-on Improvements

3.4 Ritual Use

4. Conclusion

Notes

This ancient enigmatic disk probably depicts the midnight culmination of the Pleiades for calendar leap months and festival celebration.

In 1999 a 12.6" diameter bronze disk was discovered by treasure hunters which has turned out to be widely accepted as the most ancient depiction of the sky known, including even all of the constellations shown on the walls of Egyptians temples. It has gold-leaf circles (stars) inlaid on a dark background. It has been dubbed the "Nebra Sky Disk" (often spelled Nebra Sky Disc) because it was found near Nebra, Germany.

Fig. 1. Nebra Sky Disk.

Recently, when the modern interpretations came to my attention, it became apparent that it has not been explained very well to the layman in easily accessible articles. This article seeks to remedy that deficiency by suggesting exactly how it was most likely used. Let's first look at the disk itself and then consider possible interpretations and uses.

1.1 Current Status

It has two of what had been three curved arcs attached. Two were apparently on opposite edges, but one of those has been lost although its former location is clearly indicated. The third arc has a different curvature and is also located on the edge about halfway between them on the circumference (See Figure 1). Many small holes perforate the edges as if it had been nailed a wall at some point, perhaps after it was forgotten how to use it.

1.2 Added Upon

Fig. 2. The original sky disk.
(Click to see the later stages.)

What might be a big clue to the use of the disk is the fact which has been established that at least two additions were made to the original disk. Figure 2 shows what is thought be the original disk. Then the two side arcs were added later as shown by clicking on Figure 2. Besides looking at the purity and origin of the gold, it is fairly obvious that they were a later addition because one star was shifted in position to accommodate the left arc and two stars were covered by the right arc.

Archaeologists have concluded that the bottom arc was added last (shown by again clicking on Figure 2). So what are these additions all about? Did someone think they enhanced the disk or made it easier to understand or use?

To me any explanation of what all of this means should include (1) what the original disk was intended to represent, (2) why were the two side arcs added, and (3) what was the last arc and why was it added? None of those questions have been addressed in the papers read during the minimal research done to prepare this article.

So what is this sky disk all about? What was its use if any? Was it simply a decorative wall hanging as it is becoming in our society? It was very costly to make, having gold celestial objects, so why was it made and even added upon in later years? Let's look first at current theories and then at a proposed interpretation, complete with explanation of the additions.

2.1 General Agreements

Summarizing about ten articles on this subject, here is what scholars seem to agree on:^[1]

• It is a depiction of the sky.
• The crescent represents a waxing crescent moon. This alone means that proper orientation of the disk is with the crescent on the right side if it is to depict the sky in Germany as would been seen by holding the disk vertically and facing south in the evening.
• The dots represent stars.
• The cluster of seven dots represents the star cluster called the Pleiades, the Seven Sisters. This cluster was known to the ancients and was extremely important to them. It still is today: if you own a Subaru (which means "Pleiades"), then it is shown on your hubcaps! This identification confirms the correction orientation of the disk because the Pleiades are usually slightly above the path of the moon.
• The two arcs on the sides represent the extent of the angular swing of the rising and setting of the sun between the summer and winter solstices. That is confirmed by the fact that each has a 82° arc, which indeed matches the actual annual variation in rising and setting angles at the latitude of Mittle burg (latitude 51°) where it was found.^[2] This alone implies that the designer had a good understanding of observational astronomy, much better than most readers of this article! Not bad for 1600 BC!

Here's what is not agreed upon:

• Does the circular object in the sky represent the sun or moon? Most say the sun. Either way it really begs an explanation: why would there be two moons in the sky or why would the sun be up at night?
• Do the stars other than the Pleiades correspond to known stellar objects such as planets or stars? Or are they just randomly scattered about to indicate that it is the night sky?
• Just what is the curved object at the bottom of the disk? Most say it is the solar boat which in Egypt represented the journey of the sun beneath the earth after setting in the west each night so the it could rise in the east each morning. But why was it added to the disk? What new information is it trying to share with us?
• Is the actual phase of the crescent (about 5 days old) important or not? It definitely is not the very thin crescent associated with a new moon. It might simply be an artist's choice.

2.2 Best Explanation

One explanation has appeared which claimed to be the definitive interpretation. Indeed, it still seems to be the best explanation. Let us look at what little detail could be found in a quick Internet search because it appears to be correct. Then it will be explained in detail.

Babylonian astronomers explain Nebra Sky Disk!

A group of German scientists worked together to explain the Nebra Sky Disk. Ralph Hansen, an astronomer from Hamburg, felt that the precise age of the moon shown (5 days) might be important. Here is the best account known to me of what he found when he consulted Babylonian sky lore compiled about 1,000 after the accepted age of the disk:

"I wanted to explain the thickness of the crescent on the sky disc of Nebra because it is not a new moon phase," said Hamburg astronomer Ralph Hansen.

In his quest to explain why the Nebra astronomers created a sky map with a four or five days old moon on it, Hansen consulted the "Mul-Apin" collection of Babylonian documents from the 7th and 6th centuries B.C.

These cuneiform writings represent, according to Hansen, a compendium of "astronomic knowledge from the earliest times." They also contain a calculation rule for the crescent that looks strikingly similar to the one from Nebra.

According to the ancient Babylonian rule, a thirteenth month should only be added to the lunar calendar only when one sees the constellation of the moon and the Pleiades exactly as they appear on the Nebra sky disc.^[3]

That is a painfully brief summary of the theory, intended for our modern age where very little is understood by the layman about even the basics of the motions of the sun and moon. Fortunately, after a little reflection to understand how it could work, that theory appears to be essentially the correct explanation of the the use of the disk. The reason for such certainty is that it explains the age of the crescent being 5 days and also what the other moon or sun figure is doing in the middle of sky. It also explains how the disk would have originally have been used before the addition of the three arcs, and why they were later added. Read on if you want to know how this all fits together.

There are two concepts required to understand this Babylonian "Pleiades Rule" as it is hereby dubbed. First, one should understand what problem needs to be solved, and second, one should understand how the Pleiades Rule solves the problem. Let's look now at both.

3.1 Problem: Intercalation

Our Gregorian Calendar always has exactly twelve months in a year. One reason for that simplicity is Julius Caesar basically punted the problem of getting the lunar moon and solar year both to come out even. His Julian Calendar (later to become the modern Gregorian Calendar) really only tracks the sun. If you want to know the phase of the moon, get a calendar with the little pictures of the moon on it.

Before his time, the word "month" ("moonth") meant "lunar month". It tracked the moon. The first day of each month was either on or shortly after the new moon, and the 15th of the month was usually the full moon. The cycle through the moon's phases takes about 29 ½ days, so a lunisolar calendar has months which usually alternate between 29 and 30 days so that the average month length was 29.5 days.

A lunisolar calendar also tracks the seasons of the sun, so that the year always starts at the same season. Thus, it is called lunisolar (luni="moon", solar="sun").

The problem is that a solar seasonal year is 365.24 days long and 12 lunar months are only 354.37 days long. That means that twelve lunar months are about 11 days short of being a solar year! That is the problem.

The usual solution is to insert an extra thirteenth month about every three years. The process of inserting "leap" months is called "intercalation", meaning to insert extra time units into a calendar to make two different periods come out even.

Table 1. Lunisolar calendar intercalation.

Table 1 shows how intercalating an additional lunar month every three years helps the lunisolar calendar to reconcile the differences in the length of twelve lunar months and solar year. Suppose that the new moon of Year 1 occurs on a day we call 0 on a true solar calendar, like the Gregorian Calendar. After one lunisolar year of 354 days, Year 2 will begin eleven days earlier in the solar year (on day -11). Year 3 will begin eleven days earlier than that on day -22 on the solar calendar and after 12 more months, the next year would be scheduled to begin 33 days earlier in a solar year than did Year 1!

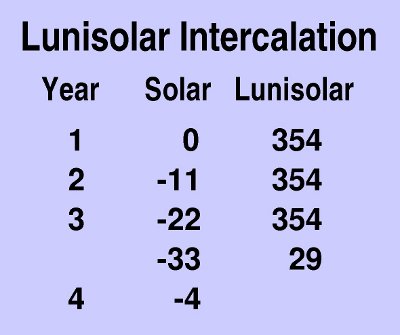If we have some way of knowing the season, such as that the snow has melted already, or if we knew the precise length of the solar year or knew of the Pleiades Rule soon to be described, at this point we can decide to make up most of that deficiency by adding another month of 29 (or 30) days. Then we would only be 33 - 29 = 4 days short. This result is the usual case with a lunisolar calendar. Whenever one leap month is intercalated into three lunisolar years, the day on a solar calendar on which the next year begins usually occurs four days earlier in the solar year. For example, if Year 1 had begun on 6 April, Year 4 would probably begin on 2 April.

From this one can see that simply intercalating one month every three years won't work because 4 days is not close enough. The Hebrew Calendar is a lunisolar calendar. It has the set scheme called the Metonic cycle of intercalating seven months every nineteen years (slightly modifying what would have been 6 months every 18 years using the every third year rule). That has worked so well that Hebrews feel it is still close enough after having been used for nearly 2,000 years. The discovery of the Metonic cycle is attributed to the ancient Greek astronomer Meton of Athens. He introduced that calendar system in 432 BC.

But what about those using the Nebra Sky Disk? Meton lived some 1200 years after that disk was buried! What other method might have been used way back then to know when to intercalate a lunisolar calendar? That brings us to the Pleiades Rule.

3.2 Solution: Pleiades Rule

The first problem to be solved is to have some independent way to know when a solar year has passed so as to know when the leap month is needed. One way is to check whether crops have ripened or any other sign of a season has come. But we all know there are early springs and late springs and it is tough to know exactly when a season starts by the weather.

Fig. 3. Which one is the Nebra Sky Disk crescent?
(Click for all phases.)

In the ancient world where the sun appeared to revolve around the earth (as it indeed still appears!), one could note that the stars also appear to revolve around the earth not only daily, but also annually. The two periods are very close to each other, one sidereal year ("star year") being 365.26 days instead of 365.24 days for a seasonal year. This difference adds up to about 1 day every 72 years, meaning that if one uses a star to align with the first day of each year, then that first day will creep one day forward on a solar calendar every 72 years. But that might be acceptable when the annual beginning of the year of even a perfect lunisolar calendar already varies by nearly a whole month compared to a true solar calendar! On the other hand, if those using the Nebra Sky Disk wanted to track the star year, then aligning with a star gives exactly the right answer.

Thus, the first step to the Pleiades Rule is to choose a star to line up with every year. The Egyptians chose the star Sirius (the Dog Star), the brightest star in the sky. Another excellent choice is the Pleiades (Seven Sisters) star cluster. The Pleiades is easily found and recognized all over the world was a very important group of stars. It is always counted as seven even though only six are visible to most people. It also has huge religious significance and has been thought by some people to be a central point about which our sun revolves.

In the case of the Nebra Star Disk, the Pleiades is probably the best choice of any star or stars because it can be recognized by even the most astronomically illiterate people, such as us moderns! Fortunately, there has been no debate that the seven little stars on the Nebra Sky Disk represent the Pleiades! That's not bad considering they are still arguing over whether the big circle is the sun or moon!^[4]

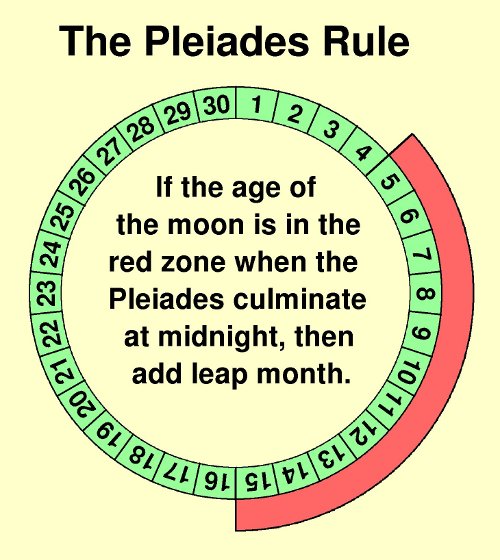
Now that we have our star picked, how do we line up on a star? The goal is to know where that star is exactly on the same day every year in place of knowing just where the sun is on any given day of the year. One simple way is to pick the day on which it is at its highest above the horizon, due south on the north-south line overhead called the "meridian". That is called the "culmination" of the star. A good day to choose is the day on which the Pleiades culminates right a midnight. Every night the cluster would be due south about 4 minutes earlier than the preceding night, so one can easily know on what night it is due south at midnight if he knows (1) where due south is and (2) when it is midnight.

Fig. 4. Egyptian Water Clock.

It is clear that the users of the Nebra Sky Disk knew due south. The two arcs representing annual swing of the sun between summer and winter on the sides show that they knew east and west accurately, being the midpoints of those arcs. South is simply perpendicular to that line.

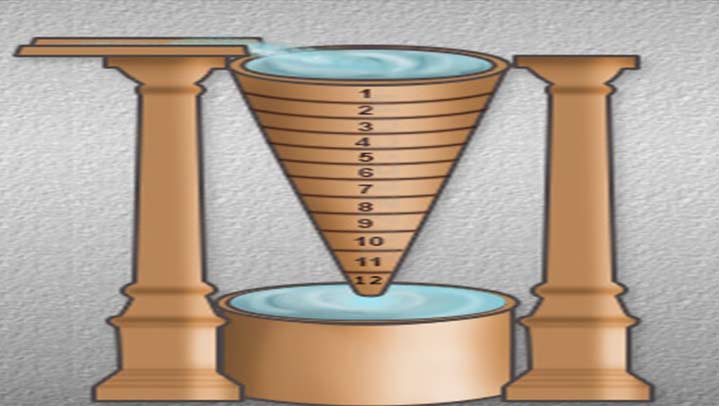As for midnight, whereas the sundial works great in the daytime, variations on hour glasses and water clocks have been known and used throughout history to measure the hours of the night (see Figure 4). Anyone with the astronomical sophistication to create the Nebra Sky Disk would certainly have had some way to measure time during the night.

If the moon happens to be full, there is an easy way to see when it is midnight (local sundial time--no time zones or daylight savings!). A 100% full moon is exactly opposite of the sun in the sky, at least in time. When it is midnight sun time, it is noon moon time. That means a full moon will be at its highest due south (culminating) exactly a midnight. So there we have one natural marker: the full moon will be either directly under or possibly even obscuring the Pleiades (as it does every 18 years) right exactly at midnight. That's great, but it only works if the moon happens to be full on the same night the Pleiades culminate at midnight.

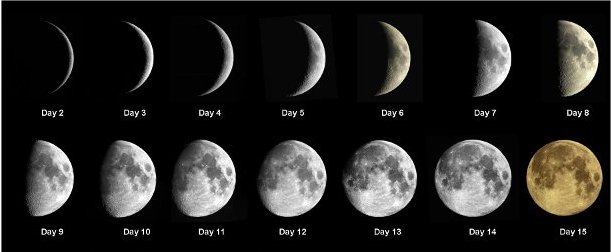
We are almost done. All that is needed now is the knowledge that a lunisolar year begins eleven days earlier every solar (or star) year. Therefore, it is desired to mark off an eleven day area of sky to know when to intercalate a month. Since we already have one marker of a full moon, we can pick the other marker on the 11th day earlier. The full moon occurs on the 15th day of the moon (the middle day of 29), so we can count back ten days to the 5th day of the moon for the other marker. Aha, there it is! The fifth day of the moon, exactly what is shown in the Nebra Sky Disk! (See Figure 3 to verify that the disk has a near perfect representation of lunar Day 5!)

Fig. 5. The Pleiades Rule.

So here is the Pleiades Rule: If on the day of the culmination of the Pleiades at midnight the moon is on Day 5 through Day 15, then intercalate a month this year. It is illustrated in Figure 5. Here's an example of how it works. Suppose that in first year the moon is near the middle of the red range, say on Day 10. A month is intercalated leaving it still at Day 10 (or Day 9 if 29-day leap month). After twelve lunar months the moon will arrive at Day 10 eleven days before the Pleiades culminate. The result is the the moon will be at Day 21 (11 days later) when they do culminate one solar or sidereal year since the previous midnight culmination. Thus, every year the phase of the moon will increase by about 11 days. After another year the phase will again increase by 11 days to Day 32, which is the same as Day 2, so there is no intercalation that year either. The next year will fall on lunar Day 13 so that third year is intercalated. As another example, if the moon is near the end of the red zone, such as on Day 14, then the next year is Day 25 and the next Day 6 (same as Day 36) in the red zone, so in that case the intercalation is after only two years. Note that it can never skip entirely over the red zone because that zone is 11 days long.

After all of that explanation, look at the first version of the disk and find everything needed to represent the essence of the Pleiades Rule. There are the easily recognizable Pleiades and a bunch of stars randomly placed to show it is night time. There is the moon at 5 days and a full moon at 15 days to illustrate the two limits. It might never have occurred to the maker than anyone might think the big gold circle was the sun, because the sun is not up at night! The Pleiades are shown between the two moons and in the south and also slightly above both moons where they are actually found in the sky.

3.3 Add-on Improvements

Fig. 6. The soltice arcs added.

As years passed some young wizard or wise man might not have thought it was obvious which side of plate was up or what direction to face to use it. Thus he added the two golden arcs on the sides to make it obvious that the side to the right of the crescent moon is west and the other side is east, so that holding it up, one must face south. He understood that all of the stars were just randomly placed except for the Pleiades, so he had no problem covering up two stars on the right and shifting one slightly on the left. That is a big clue that whoever added the two arcs did not think the exactly placement of those stars was critical.

That implied precision to face exactly south helps make it clear that it is depicting the culmination of the Pleiades. They might have been shown exactly on the center line of the disk, but apparently could not be there because there needed to be room for the entire full moon to be shown. Even with the Pleiades shifted slightly to the right of a vertical center line (the meridian), the full moon is still shown smaller than the crescent to fit it in, which the maker likely didn't think would be a problem for anyone. Figure 6 shows the addition of the two solstice arcs. We might have written a capital W (for West) on the right side and E (for East) on the left to indicate the same thing. But of course, that would require the user to know our alphabet and the words East and West. Whoever added those two arcs was entirely successful because our modern viewers figured that out.

Fig. 7. Solar boat added.

Then perhaps it was his grandson wizard who came along and didn't think it was so obvious that this observation was to be made at midnight. He wasn't born knowing that and thought it should be included the picture so that so the disk would be self-contained, needing no instruction manual.

So stop and think: what would you do to signify that the time to use this disk is at midnight? We now use lots of little icons to be understood internationally, but what do we have for midnight?

Fig. 8. Egyptian solar boat

Whoever made this apparently decided that surely any educated person would know about the symbolism of the solar boat carrying the sun after sunset from the western horizon around to the eastern under the earth during the night (see Figure 8). What better way to show it is to be used at midnight than that show the solar boat, representing the sun, at the bottom of the disk halfway around the circumference between to two arcs which represent where the sun rises and sets every day of the year? Thus, the purpose of the solar boat is to show that the culmination of the Pleiades occurs at midnight.

Not bad for primitive man, wouldn't you say? Especially since modern experts can't agree on much more than what was stated above, which did not even include whether the round object was the sun or moon! Thanks must be given to astronomer Ralph Hansen for going to the effort to discover a partial statement of a Babylonian version of this proposed ancient Pleiades Rule. Without the clue that it had to do with intercalation, the disk may never have been deciphered in our modern age of atomic clocks and very few sundials.

3.4 Ritual Use

A question arises from the foregoing explanation. Why didn't these people just use the sun, rather than a star? They obviously knew all about the course of the sun because the solstice arcs are 82°, which is correct length for the Mittelberg. That means they knew east and west accurately (the midpoints of those arcs). While the length of the year can be determined by solstice observations (21 Jun or 21 Dec), such as at Stonehenge, it is more accurate to observe the sun at the equinoxes (21 Mar or 23 Sep) when the sun is racing along the horizon.

An example of this is the Hebrew Calendar, which is also a lunisolar calendar. Today it is self contained, based on the Metonic cycle, so no observations are needed. But previously, with the observational Judean Calendar, the rule was that Passover could not occur before the spring equinox. That works perfectly and never gets out of sync with either sun nor moon. Anyone sophisticated enough to have figured out the Pleiades Rule would have known this.

So why are these people literally up in the night making these observations? This is not my area of expertise (astronomy and calendars), but perhaps a few suggestions can be made that could lead to further research.

Halloween comes from the Gaelic Samhain festival.

Many people in tune with nature celebrate annual celestial events with feasts and festivals. Somehow it sounds more fun to build a big bonfire and watch the moon sometimes actually occult (block out by moving in front of) the Pleiades at midnight. If a feast is included, that might rival watching the rising sunlight go down a shaft to light up the back wall of a temple. The latter would only be visible to a very few, but everyone in Europe could watch an occultation of the Pleiades. Thus, it is suggested that the Nebra Sky Disk was used for feasts and ceremonies.

Another possibly use has to do with the Gaelic (Irish) harvest feast of Samhain (pronounced SAW-win or SOW-in), which marked the beginning of winter on the cross quarter day of 31 Oct, about halfway between the autumn equinox and winter solstice. For some it marked the new year, so that would be a perfect time to check to see if a leap month were needed. It is the forerunner of Halloween ("All Hallows Evening" because 1 Nov is All Saints Day). The Pleiades would have culminated at midnight on 31 Oct (Julian) about AD 650. But in 1600 BC the midnight culmination of the Pleiades would have occurred on 1 Oct (Greg.), so that would probably not have been tied to Samhain at that time.

Another suggestion is that there are accounts that when the Spaniards conquered the Aztecs, they were performing a ceremony every 52 years when the Pleiades culminated at midnight, where it was felt they needed to sacrifice a man in order that the universe not come to screeching halt! That is the type of tradition which could have degenerated from a true principle about intercalating a calendar to keep everything running correctly.

It seems this idea of watching the Pleiades culminate at midnight has widespread cultural expressions and if so, it sure sounds like they had a common source. Moreover, they might have lost the original Pleiades Rule and just kept up the celebration!

Notes