a defender must return to play even against
an attacker who makes a fraction a of his shots.
by John P. Pratt
Aug 17, 2000
© 2000 by John P. Pratt. All rights Reserved.
We have all seen developing players who were so eager to attack that they only made about half of their "winner" shots, and hence lost a lot of games. In fact, at some time in our table tennis career, we probably have played that way ourselves. After losing a few times, it finally dawned on us: "Duhh, I'm beating myself! I've giving my opponent so many points that he only has to return a few shots to win!" How can you make sure that you are not beating yourself?
One player I practice with was working on developing his attack and missed so many shots that he was easy to beat. We play at work where the winner stays on the table, so we don't have the luxury of just practicing, because people are waiting. He didn't mind losing because he was improving. Now he makes over half of his "kill" shots and suddenly he is very hard to beat. The effect was dramatic: he lost when he made about half, but then he began to win with only slightly more than half because I could not return very many. So the question arose, "What is the minimum fraction of shots an attacker must make so that he's not beating himself?"
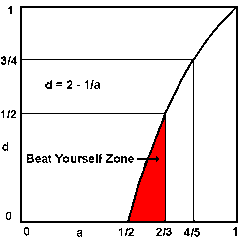
Having a degree in mathematics, I decided to try to calculate the minimum fraction of successes that an attacker should make to ensure that he has a good chance to win. I found this problem interesting because the answer wasn't obvious. What is obvious is that if someone only makes half of his shots, his opponent doesn't have to do anything at all to play even. Clearly, an attacker must be aggressive enough to force the defender to miss, and yet not try so hard that he misses too many attempts himself. And it is also obvious that if the attacker can make every shot, the defender must also make every shot to play even. But what about other values? That is, if an attacker makes a fraction a of her shots, what fraction d must the defender return in order to keep playing even? The answer is shown in the following graph for every fraction of shots the attacker might make.
 |
|
Figure 1. d is the fraction of shots a defender must return to play even against an attacker who makes a fraction a of his shots. |
In Figure 1, the numbers on the horizontal line represent the fraction of successful attack shots (a, for attack). The numbers on the vertical axis shows the fraction of those shots the defender must return to play even (d, for defense). The dark curved line shows the answers for all values of a and d. It starts from the point on the bottom where a = 1/2 and d = 0, meaning that if the attacker only makes 1/2 half of her shots, the defender only has to return 0 of them to play even. We knew that to start with, and we also knew the point in the upper right hand corner, that if a = 1, meaning the attacker makes every shot, then d = 1 also, meaning that the defender must make every shot. Now let's look at the points in between those extremes.
You can see that most of the good from making your offense shots comes in just raising the fraction of successes up to 2/3. The curve rises very steeply at first, so that if a player makes 2/3 of her attacking shots, the defender must return half of them to play even. So as my friend was able to increase his percentage from 50% up a little bit to 67% (that is, to 2/3), what surprised me was that I had to increase my returns from 0% all the way up to 50%, just to play even. That point, where the defender must return half of the attack shots seems like a good place to define as minimum fraction that an attacker must make. That is, if the defender doesn't even have to return half of your shots to keep playing even, then you are in the "Beating Yourself Zone," shown in red in the graph. On the other hand, if you can make at least two thirds of your "winners" that are good enough that half of them don't come back, then you have a good chance of winning. For those interested, the exact equation and the derivation are also given.[1]
So do I expect you to understand all this math, or to carve this graph on the handle of your paddle to refer to in the middle of a game? Not at all. But if you will memorize just the one middle point on the graph, it could help you as it has helped me. I'll state it in the form of a rule:
If an attacker can make a minimum of 2/3 of his shots |
This rule is illustrated in the scores in the following sample game. The attacker's hits are in bold, the defender's in italics. Note that 2/3 of attacker's shots are hits, whereas only half of the defender's are hits. Only the shots are recorded where the attacker begins to attack. To illustrate the idea, it is assumed that they play even otherwise, such as when either of them is serving. Thus, all of the points shown begin with the attacker, no matter who is serving. Moreover, there could be other points in between these offense/defense exchanges, perhaps with both players pushing for a few shots. The point is, that during the offense/defense portions, the score will increase evenly if the attacker makes two out of three shots and the defender one out of two.
| Description of Point | Score | Remarks |
| Hit, Hit, Hit, Miss | 1-0 | |
| Miss | 1-1 | These last two points could repeat forever |
| Miss | 1-2 | |
| Hit, Hit, Hit, Miss | 2-2 | These are the same as the first two points reversed |
| Hit, Miss | 3-2 | |
| Hit, Hit, Miss | 3-3 | Or these last two points could repeat forever |
| Hit, Hit, Miss | 3-4 | |
| Hit, Miss | 4-4 | These are the same as the last two points reversed |
| (Continues) | (even) | Every pair of lines completes the 2/3, 1/2 ratios |
|
Table 1. A sample game. The Attacker's shots are in bold and the defender's in italics. Note that 2/3 of the attacker's shots are hits, and only half of the defender's, yet the score stays even. | ||
Thus, an attacker must make a minimum of 2/3 of his aggressive shots to avoid beating himself. And if those shots are good enough that they have less than a 50-50 chance of coming back, then he will be on the road to winning.
Now let's look at a simple way to apply this rule in a real match. Suppose you notice that both you and your opponent are about equally good at pushing and the tournament match is turning into a pushing contest because you are both afraid to attack. Here is a simple experiment you can try to see if you should grab the offense. Try attacking two or three times. If you can make two of your first three attempts and if your opponent only can return one of your two successful attempts, then it is definitely worth trying some more offense. This is especially true because having been successful even at first, you will probably loosen up, gain more confidence, and be even more successful as you continue to take the initiative. After your first three attempts, you don't have to continue keeping track of percentages in the game because the score will do that for you. The usefulness of this rule is to get a good indication of how the score will turn out before it is too late to change your tactics.
If 2/3 is the minimum fraction of shots for an attacker to make to avoid self destruction, then what is the ideal percentage for the attacker to try to attain? Clearly we all want to hit a very high percentage of our shots, but if we try to get 100%, never taking a chance, then we run the risk of being so conservative that we have no "winners" at all. Looking at the graph in Figure 1, we see that as the attacker's percentage increases, so must the defender's. For example, if the attacker makes 4/5 of her attempts, then the defender must return 3/4 of them to keep playing even.
Once you are above the "Beating Yourself Zone," the best percentage to shoot for will probably depend on the opponent you face in any given match. That is, you will probably have to decide as you see how many shots are returned. Different coaches will probably have various opinions about what is the ideal percentage to attain to be a champion. But one thing is now clear: If you cannot make 2/3 of your attacking shots, then it won't matter who your opponent is, because you'll be beating yourself. Hopefully, remembering this "Attacker's Minimum" will help us all to improve our odds of winning more consistently.
(1-a) + ad[(1-a) + ad[(1-a) + ad[(1-a) .....]]] = 1/2(1-a)(1 + ad + (ad)2 + (ad)3 + ...(ad)n .... = 1/2 (where the number of terms approaches infinity for long rallies).
(1-a)/(1-ad) = 1/2 (summing the infinite series, from college algebra).
2(1-a) = 1-ad
d = 2 - 1/a.