 |
Realigning the hands of a watch is simple because there are an exact number of seconds in a minute and an exact number of minutes in an hour. Thus, the first realignment interval encountered is a perfect lineup, and there is no reason to search for more accurate intervals.
A calendar can be thought of as a clock that keeps track of longer periods or cycles of time the sun and moon are like the hands of the clock. Note that our word "watch" (meaning clock) is the same as that formerly used to describe a time period determined by "watching" the sky (as in Matt. 24:43). A problem that arises is that sometimes the cycles do not 'come out even. For instance, the solar year, in which the seasons repeat, equals 365.2422 days rather than a whole number of days such as 365. A question fundamental in the construction of any calendar is how to align the different cycles. The solution lies in finding an interval that is approximately a whole number of all the cycles.
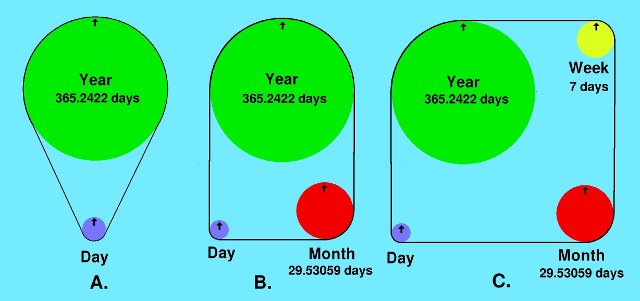 |
The problem can be represented by the device drawn in Figure 2a. The large pulley has a circumference equal to 365.2422 times that of the smaller one. If each one has an arrow painted on it that points exactly vertical, after how many revolutions will both arrows be pointing straight up again?
Because the circumference is an irrational number of days, as is the case with most astronomical periods, the two pointers never again point straight up exactly simultaneously. There are only approximate solutions; the longer one is willing to wait, the more accurately they will align.
For example, after 365 revolutions of the small wheel, the larger one almost (but not quite) finishes a rotation, so a first approximation to a year is 365 days. But after 1,461 revolutions of the small pulley, one might notice that the large one has more nearly completed exactly four turns (years). That gives an average year of 1,461 divided by 4 = 365.25 days, which is the reason we add a leap day every 4 years. Our Gregorian calendar is based on the observation that 146,097 days very nearly equal 400 years, giving an approximate year of 146,097 divided by 400 = 365.2425 days.
A realignment interval for the set of pulleys is a number of turns of the smallest one which brings all of the arrows back to the vertical point better than any smaller number of turns.
The seemingly simple problem of finding a realignment interval for several cycles is, in fact, a very difficult problem in number theory;* fortunately, however, it is easily solved with a computer by 'brute force" by simply checking every possible combination of numbers for the best fit.
For our solar calendar, 4 years is a realignment interval, whereas 400 years is not because there is at least one better solution with a smaller number of years (12,053 days divided by 33 years = 365.2424 days).
Figure 2b depicts the more complex problem of realigning the lunisolar calendar, which also includes the lunar month, the period of the moon's phases. The modern Hebrew calendar employs a realignment interval, called the Metonic cycle, that has been known since at least five centuries before Christ: 19 years very nearly equal 235 lunar months. This means that the lunisolar calendar requires leap months as well as leap days.
Figure 2c represents the problem of realigning the Jewish calendar described in the text, also including the week as a cycle. The realignment intervals include 68, 152, 220, and 372 years. For example, in this century Easter falls on 3 April, 16 Nisan (Jewish) in the years 1904 and 1988, being 68 and 152 years after 1836, respectively. For longer realignment intervals, the variable lengths of the year and day must be considered. The realignment interval of 1,803 years discussed in the text is better than any other until 5,382 years have elapsed.
*The "best fit" criterion is that the distance the belt must travel to align the worst pulley must be smaller than the corresponding distance for any smaller number of turns. This criterion was adapted from H. R. P. Ferguson and R. W. Forcade, "Generalization of the Euclidean Algorithm for Real Numbers to All Dimensions Higher Than Two," Bull.of Am. Math. Soc. 1 (November 1979), pp. 912-14.