The Saros

by John P. Pratt

Index, Home, Main Article

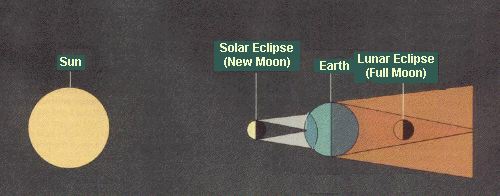
Perhaps the greatest contribution to astronomy from ancient Chaldea was the discovery of a period of 6,585 days (18.03 years) called the saros, after which eclipses might repeat.*

An eclipse occurs when the sun, moon, and earth form a straight line. Solar eclipses occur at a new moon, when the earth is in the moon's shadow; lunar eclipses are at full moon, when the moon passes into the earth's shadow. (See Figure 1.)

Figure 1, A solar eclipse can occur at a new moon, or a lunar eclipse at a full moon, when the sun, earth, and moon are approximately in a straight line. The reddening of a lunar eclipse is caused by light being refracted into the earth's shadow by the atmosphere. Note that a total solar eclipse is only visible to the small area of the earth in the center of the new moon's shadow, whereas a total lunar eclipse can be visible to the entire night-time half of the earth.

Figure 2. The saros (18.03 years) is a realignment interval after which eclipses may repeat. It realigns the periods in which the moon is at the same phase (such as new or full), at the same distance, and at the point of intersection of the moon's orbit with the sun's apparent path. Eclipse cycles can only reoccur when the sun, moon, and earth are once more in proper alignment-illustrated here by all three arrou;s pointing nearly straight up again.

For a given series of eclipses to reoccur, three conditions need to be fulfilled:

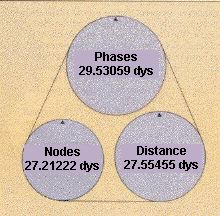1. The phase (full or new) of the moon must be the same, which is why similar eclipses are always separated by a whole number of lunar months of 29.53059 days.

2. The moon must be near the place where its path crosses the sun's apparent path. The period of such crossings is 27.21222 days.

3. The moon needs to be at about the same distance from the earth in order to completely cover the sun in total solar eclipses. (The moon's distance from the earth changes because its orbit is not circular, which makes its apparent size vary by about 10 percent.) This reoccurs in intervals of 27.55455 days.

Thus, the problem of predicting when eclipses will repeat is a question of finding a realignment interval for those three cycles. (See Figure 2.) After an eclipse, when will all three cycles again coincide? One of the very best realignment intervals is the saros of 6,585.32 days.

As discussed in the text, the return of Elijah occurred 100 saros periods after the proposed date of the Savior's resurrection.

*Arthur Berry, A Short History of Astronomy (New York: Dover, 1961), p. 19. The Babylonians are known to have been aware of the saros since at least several centuries B.C. It is not known whether such knowledge dates back to the time of Abraham, who lived in that same area about 2000 B.C.