by John P. Pratt
24 Nov 2014, 1 Elul (UH)
©2014 by John P. Pratt. All rights Reserved.
| 1 Same Pattern as Hebrew |
| 2 Uniform Enoch Calendar Ties |
| 3 Uniform Enoch Seasons |
| 4 The 33-Year Wheel |
| 5 Two Versions |
| 6. Correlation |
| 7. Conclusion |
| Notes |
In the three decades that this sacred calendar research has been continuing, thirteen sacred calendars have been discovered which are apparently used for timing key religious events. During this last year it has become clear that many of the calendars have both a "normal" version which tracks the average position of celestial bodies and also a "uniform" version which uses the same pattern without any variation such as leap days, which does not actually track those bodies at all. One advantage of a uniform calendar is that when one date is known from history, then every date in history is determined.
During the last month research was done to determine whether or not the Hebrew Calendar, which tracks both the sun and moon, has a uniform version. The purpose of this article is to announce that there is indeed compelling evidence that such a calendar exists, and is used to time key religious events. In fact, it has an accompanying secondary version. Moreover, it was clearly designed to be synchronized with the Uniform Enoch Calendar, which also has a secondary version.
Technical calendar details are presented in this article, which is recommended only for serious calendar enthusiasts. The results concerning religious history will be published soon hereafter, which should be of interest to a larger audience. Usually both are presented together, but this time there are so many technical details as to merit a separate article.
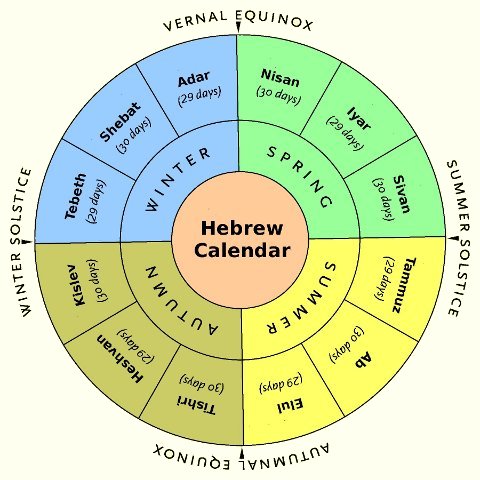
If there is a Uniform Hebrew Calendar (abbreviated UH) that is being used to time religious events, and if it follows the precedent set by the other uniform calendars, then one would expect it to use the same year lengths and patterns as the Perpetual Hebrew Calendar. That calendar is nearly identical to the tradition Hebrew Calendar except minor corrections have been made for long term drift. They both, however, use the same year lengths and allowed starting days.
 |
Alignment with the week is done by restricting New Year's Day in the spring to only occur on alternating days of the week: Sunday, Tuesday, Thursday, and Saturday. In order to fulfill all of these requirements, there are 6 different year lengths used: 353, 354, and 355 days in normal years, and 383, 384, and 385 days in leap years. The years with 353 or 383 days drop one day from the 9th month (Kislev) and those with 355 or 385 add one day to the eighth month (Heshvan). Other than those two months, the other months always have the same number of days. The leap month always has 30 days and is inserted just before the final month Adar. It becomes Adar and the final 29-day month is Adar 2 or Veadar.
The illustration shows New Year's Day on 1 Nisan aligning with the spring (vernal) equinox (20 or 21 March, when the sun rises nearly due east). Because of the occasional addition of an entire month, that is only approximate, but the intent appears to be that 1 Nisan should fall within a two-week period of the equinox. The rule from back when the Hebrew Calendar was determined by actually observing the moon is that 15 Nisan (Passover) must never occur before the equinox. To prevent it, the leap month was inserted at the end of the previous year.
For some purposes the day 1 Tishri (Rosh Hashanah) near the autumn equinox is considered to begin the year, as it does on the modern Hebrew Calendar. But in my articles 1 Nisan is referred to as New Year's Day and 1 Tishri as the Feast of Trumpets.
A Uniform Hebrew Calendar would be expected to used these six year lengths aligning with the week in a similar fashion, even though there would no longer be a requirement to align with either the sun or moon. It should also have the same months and holy days and appear to be almost identical to the Hebrew Calendar. And it should probably have the 24-hour day begin at 6 pm as does the Hebrew Calendar. All of these points turn out to be true of the calendar proposed in this article.
When research was initiated to see if a Uniform Hebrew Calendar may exist, there were several bits of evidence that supported the notion strongly. The most compelling in theory was the possible synchronism with the Uniform Enoch (UE) Calendar.
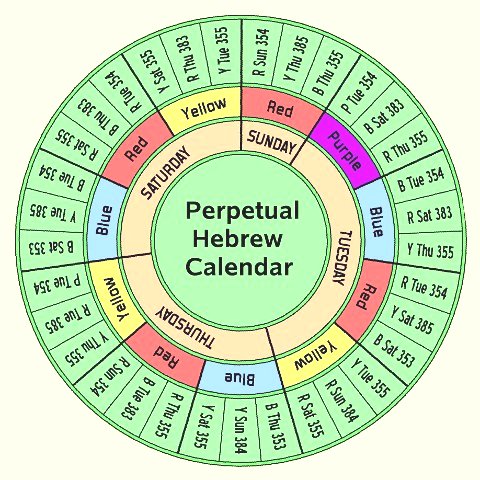 |
A Uniform Hebrew Calendar could use a similar wheel in which every set of three years equaled 1,092 days. In that case, it would stay synchronized indefinitely with the Uniform Enoch Calendar in which every year is exactly 364 days (no leap years). This possible synchronization is the first evidence that a Uniform Hebrew Calendar might, or even "should", exist.
What have the Hebrew and Enoch Calendars to do with each other? They are like two sides of the same coin. Compare the Enoch Calendar (described in the Book of Enoch) shown in Figure 3, to the Hebrew shown in Figure 1. They both align with the sun, moon and week, but the do so in a different order of precedence. The Hebrew aligns most with the moon, second with the week, and lastly with the sun. The Enoch aligns first with the week (every year begins on Sunday), secondly with the sun, and lastly with the moon. The alignment with the moon is so small that most researchers believe it is only a solar calendar. The alignment with the sun is done by adding an entire week before the spring equinox when necessary, similar to the Hebrew Calendar adding a month. Thus, it begins within about a week of the spring equinox. Each quarter of the year always begins on a Sunday. In the Uniform version, the year length is always 364 days (exactly 52 weeks, or 4 quarters of 13 weeks) because no leap weeks are added to actually track the sun.
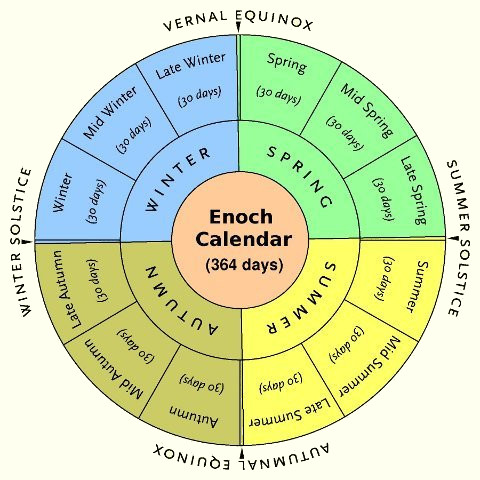 |
The second piece of evidence supporting the existence of a UH calendar is the choice of holy days in the first month of the Enoch Calendar. Three of the holy days in the first month of the Enoch Calendar are New Year's on 1 Spring (always Sunday), Consecration on 10 Spring (always Tuesday), and the Last Day of Passover on 21 Spring (always Saturday). Every year the Hebrew Calendar drops back about ten days from a 364-day Enoch year, except in a leap year when it jumps forward about 20 days (back 10 and forward 30). One possible correlation of the first day of the UH Calendar (New Year's on 1 Nisan) to the UE Calendar is the following:
Year 1 (355 days): New Year (UH) is Tue 10 Spring, Consecration (UE).
Year 2 (384 days): New Year (UH) is Sun 1 Spring, New Year's Day (UE).
Year 3 (353 days): New Year (UH) is Sat 21 Spring, Last Day Passover (UE).
Total = 1,092 days = 3 x 364 days = 3 Uniform Enoch years.
Indeed a Uniform Hebrew Calendar can be constructed on exactly such a repeating triad in which every year would begin on a holy day of the Uniform Enoch Calendar. Note that this triad starts on the same three days as the Yellow Tuesday triad shown in Figure 2. It was when this correspondence of triads to UE holy days was discovered that UH research began in earnest.
The very first model tested was this one, which was incredibly simple. Simple it was, but one could instantly see when looking at a list of 400 historical days on which key religious events occurred, that almost none of them ever lined up with the UH holy days using this model. In other words, even though it is a mathematically sound model, no one is apparently using it.
There is a serious problem with the 3-year correlation just proposed between UH and UE calendars. Both calendars represent the 4 seasons, with three months each per season. As stated above, the Enoch calendar is the more accurate to measure (solar) seasons, whereas the Hebrew is more accurate to measure (lunar) months. Both calendars are uniform, so the do not actually track the real sun and moon, but instead slowly revolve around the true seasonal year. On the other hand, if they both have years which average exactly 364 days in length, then one would expect the seasons of the UE and UH calendars to align with each other.
On the Hebrew Calendar, the day 1 Nisan is supposed to occur within a couple of weeks of the spring equinox, which on the Enoch Calendar is 0 Spring. Thus, on these two Uniform calendars, the "uniform" equinox can be considered always to occur exactly on 0 Spring (UE).
The problem with the correlation above is that the first day of every UH year would occur after that equinox (0 Spring). The way a triad is designed, it is the first year of the set of three that should be near the equinox, not the second year. Using 0 Spring (UE) to define the spring equinox, here is another way in which the two calendars could be aligned:
Year 1 (355 days): New Year's (UH) is Sat 0 Spring (UE), Equinox.
Year 2 (383 days): New Year's (UH) is Thu 22 Late Winter (UE).
Year 3 (354 days): New Year's (UH) is Tue 10 Spring (UE), Consecration.
Total = 1,092 days = 3 x 364 days = 3 Uniform Enoch years.
This correlation has only two (rather than three) UE holy days fall on New Year's Day (UH), but it has the advantage of having the UH year begin within 10 days of the equinox every year. This exact triad is labeled "Red Saturday" in Figure 2. On the other hand, even if this pattern were repeated indefinitely, the main holy day alignments would occur on 1 Nisan, which is not one of the most important Hebrew holy days, like Passover or Tabernacles. There needs to be a way to allow for more variety.
While this researcher usually begins with a very simple, utilitarian model such as the above two attempts, so far that has rarely proven to be correct. The versions used have turned out to be rich in beauty and diversity as well as scientifically accurate.
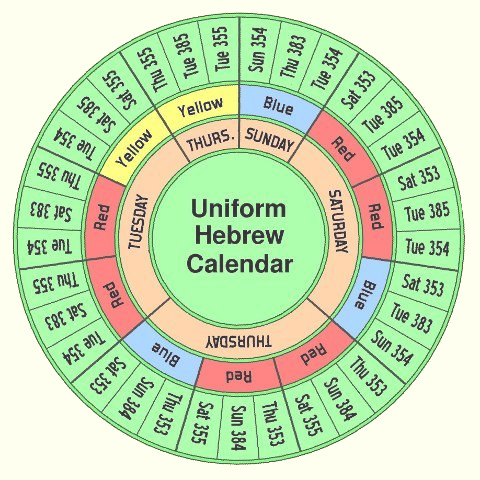 |
One important difference between the 33-year Perpetual Hebrew Calendar wheel (Figure 2) and the Uniform Hebrew Calendar wheel (Figure 4) is that because the former actually tracks the moon, the progression of days for 1 Nisan as one progresses clockwise around the wheel is always increasing the day of the week. After Sunday comes Tuesday, then Thursday, then Saturday and back to Sunday. Those are the only days on which the year is allowed to begin. Progress though that extra week means that the total number of days in the wheel is 11 triads x 1,092 days per triad + 7 (that 7 being the extra week).
In the case of the Uniform Hebrew Calendar wheel, the starting day of the year regresses from Sunday back to Saturday, as the years progress clockwise around the wheel. Then it keeps dropping back to Thursday and then finally to Tuesday as the low point. Then those lost days are made up in the last two triads as New Year's Day returns to Thursday and finally Sunday again. Thus the number of days in the wheel is exactly 11 triads x 1,092 days per triad. And thus it keeps in sync with the Uniform Enoch Calendar which has 364 days in every year, being 1,092 in three years.
Another detail has to do with the colors assigned to each triad. In the Perpetual wheel, the colors refer to tracking the moon: blue for dropping the position of the new moon during the day, red for keeping it about the same, and yellow for raising it. In the Uniform wheel, the colors refer to days of the week: blue drops the weekday starting the next year, red keeps it the same, and yellow raises it to a later weekday.
Something totally unexpected surfaced while doing this research. Not only did one excellent version of a UH Calendar appear, but a second version almost as good also appeared which differed only by beginning two weeks later. Several research days were spent trying to separate the "one true version" from the supposed impostor. But then it was remembered that the exact same thing occurred with the Uniform Enoch Calendar. When it was first discovered one version of it seemed clearly the best. Then several years later subsequent research showed that another version seemed better in that there were more meaningful alignments throughout history. And the second version also only differed from the first by two week in its starting date. The first version was deemed erroneous and was replaced by the new version.
Now exactly the same two versions, again nearly equally good, have appeared with the UH Calendar. This is too much of a coincidence to ignore, especially in two such closely related calendars.
In each case the two versions differ by 14 days. Before I attempt an explanation of why there are two versions of both the UE and UH calendars, let me make it clear that the two versions exist and are being used. The following explanation is merely my story to explain it. If that explanation is found to be inadequate, that will not negate the existence of the other versions. In other words, they were not created to fulfill this explanation; the explanation was created to explain their existence.
If one looks more closely at the results of using the 33-year wheel, on finds the following. In the first year, Sun 1 Nisan begins on 1 Spring, and 1 Tishri begins on 27 Late Summer. As the years progress around the wheel, they begin earlier in the week. The lowest is when they begin 5 days earlier, on the previous Tuesday. At that point Tue 1 Nisan is 27 Late Winter and Thu 1 Tishri is 22 Late Summer. The main point here is that near the beginning of the wheel, the first year of a triad approximately lines up with the UE year.
The receding through the year, however, brings the autumn holy days into focus: In the third year of the first triad, Tue 1 Nisan falls on 10 Spring. In that autumn Thu 1 Tishri occurs on 5 Autumn. But at the low weekday point of the wheel when the triads begin on Tuesday (five days earlier), then the third year of the triad begins on Thu 1 Nisan on 5 Spring and Sat 1 Tishri falls on 0 Autumn. Thus, at the high weekday point of the cycle the spring holy days align in the first year of a triad, and at the low weekday part of the cycle the autumn holy days align in the last year of a triad.
One really nice feature is that, as discussed above, in the traditional Hebrew Calendar, Passover must never occur before the equinox. That means Passover (15 Nisan) should never occur before 0 Spring. As the first day of Nisan regresses through the year, does it ever go beyond that point? The earliest beginning is always in the second year of a triad, and at best it starts 10 days before 1 Nisan. Then as the years progress around the wheel, it drops back 5 days, so that is cutting it very close. A check of every year of the 33-year cycle shows that the earliest beginning day is when Passover falls precisely on 0 Spring, reaching the very minimum allowed. Thus, this 33-year wheel includes great diversity and is allowed by the traditional rules of the Hebrew Calendar.
That provides a reason besides variety for the triads to regress through the week. But what about the middle year of a triad? In that year the two calendars never come close to aligning. That opens the door for the explanation of the other two calendars. Suppose there were a second UE version which only differs by beginning two weeks earlier, and a second UH version which begins two weeks later. Let's call them the "minor" versions of those calendars and the original versions the "major" versions. Then in the second year of a triad, the minor version of the UE Calendar will tend to align with the major UH, and the minor UH with the major UE.
For example, in the second year of the wheel (high weekday), on both of those opposite pairs 1 Nisan falls on 5 Spring (close) but 1 Tishri falls on 0 Autumn (bull's-eye). And at the bottom of the cycle we get in the second year of the triad that 1 Nisan falls on 0 Spring (bull's-eye) and 1 Tishri on 26 Late Summer. Those correlations precisely match those of the first and third years of triads for the two major versions. Thus, at the high weekday point of the cycle the autumn holy days align in the second year of a triad with the minor versions, and at the low weekday part of the cycle the spring holy days align with them.
That minor version of the UE calendar is precisely the one that was discovered and published first. Several years later it was discarded in favor of a better (now "major") correlation, beginning two weeks later. So now that original version is being restored as the minor UE version (UE2). Along with the minor version of the UH Calendar (UH2), it will be added with the UH Calendar to the Calendar Spreadsheet on my website.
Should the two minor versions be counted as full-fledged sacred calendars? At this point the answer seems to be no. For now they will be treated as "second witnesses" only. That is, if an event date is also holy on either the Perpetual Hebrew, Enoch, or (major) UE or UH calendars, then their witness can be used to replace the major version, if it is not on a holy day, to testify of the importance of that date. Otherwise, the will not count as a holy day in programs such as the Sacred Score Calculator of how many holy days an event falls on.
One of the most important features of any uniform calendar is the once one day is selected to line it up with our Gregorian Calendar, then every date in history is determined. By having carefully analyzed over 400 historical dates, the proposed Uniform Hebrew Calendar uses the year wheel shown in Figure 4, beginning with the Sunday triad at the top starting on Sun 6 April 4071 BC (Gregorian). Then years are determined by following the wheel clockwise to determine the length of the next year. The years are never interrupted, but simply continue to be reckoned in that manner indefinitely.
Years are counted from that starting point, so that the first year is year 0. In that way, if one wants to know where any given year falls in the 33-year cycle, one needs only to divide the UH year by 33 and the remainder will equal the year in the cycle (counting the first year as year 0 and the last as year 32).
A Uniform Hebrew (UH) Calendar has been discovered which is tied to the Uniform Enoch (UE) Calendar by following a pattern which keeps its first day near the UE spring equinox day. The UH month and year lengths are the same as the traditional Hebrew Calendar, and the order of years follows a similar pattern. The exact order of years is given by a 33-year wheel of years which repeats indefinitely. The total number of days in the 33 years is the same as the total in 33 Uniform Enoch years of 364 days each, so the alignment of the two calendars exactly repeats every 33 years.
Two other sacred calendars are also discussed. They are secondary (or minor) versions of both the UE and UH Calendars, and only differ from them by beginning two weeks earlier or later, respectively. Their use seems to be confined to be second witnesses to dates on the other Enoch or Hebrew calendars. The minor version of the UE Calendar is identical to the original correlation discovered for that calendar, which was subsequently discarded in favor of the one currently used.
This article only explained the technical details of the UH Calendar. The usefulness and sacred witnesses it produces will be discussed in a future article.